题目内容
如图,点C、D分别在⊙O的半径OA、OB的延长线上,且OA=6,AC=4,CD平行于AB,并与AB相交于MN两点.若tan∠C= ,则CN的长为 .
,则CN的长为 .
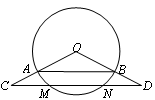
 ,则CN的长为 .
,则CN的长为 .
 +4.
+4.试题分析:过O作OE⊥CD,连接OM,由垂径定理可知ME=
 MN,再根据tan∠C=
MN,再根据tan∠C= 可求出OE的长,利用勾股定理即可求出ME的长,进而求出答案.
可求出OE的长,利用勾股定理即可求出ME的长,进而求出答案.试题解析:过O作OE⊥CD,连接OM,

则ME=
 MN,
MN,∵tan∠C=
 ,
,则
 ,
,∴设OE=x,则CE=2x,
在Rt△OEC中,OC2=OE2+CE2,即102=x2+(2x)2,解得x=
 ,
,在Rt△OME中,OM2=OE2+ME2,即62=(
 )2+ME2,解得ME=4.
)2+ME2,解得ME=4.∴CN=CE+EN=
 +4.
+4.
练习册系列答案
相关题目

 是恒成立的.
是恒成立的.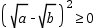 恒成立,说明
恒成立,说明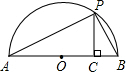
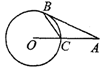

 ,母线长是6 cm,则该圆锥的侧面展开图的圆心角的度数是 .
,母线长是6 cm,则该圆锥的侧面展开图的圆心角的度数是 .
 的中点,则下列结论不成立的是( )
的中点,则下列结论不成立的是( )

