Question

【题目】为等腰直角三角形，，点D在AB边上（不与点A、B重合），以CD为腰作等腰直角，.

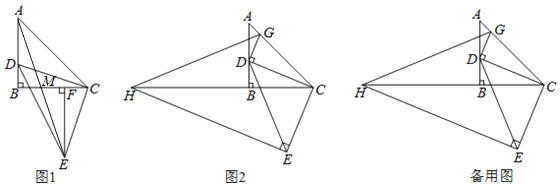
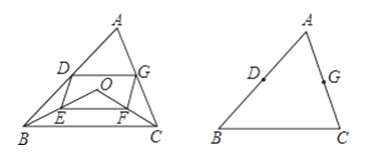
（1）如图1，作于F，求证：；

（2）在图1中，连接AE交BC于M，求的值。

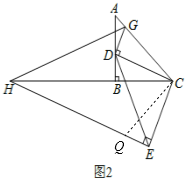
（3）如图2，过点E作交CB的延长线于点H，过点D作，交AC于点G，连接GH当点D在边AB上运动时，式子的值会发生变化吗？若不变，求出该值：若变化请说明理由.

Answer 1

【答案】（1）证明见解析；（2）2；（3）不变，理由见解析.

【解析】

（1）根据等腰直角三角形的性质得到CD=CE，再利用等角的余角相等得到∠DCB=∠CEF，然后根据“AAS”可证明△DBC≌△CFE；

（2）由△DBC≌△CFE得到BD=CF，BC=EF，再利用△ABC为等腰直角三角形得到AB=BC，所以AB=EF，AD=BF，接着证明△ABM≌△EFM，得到BM=FM，所以；

（3）在EH上截取EQ=DG，如图2，先证明△CDG≌△CEQ得到CG=CQ，∠DCG=∠ECQ，由于∠DCG+∠DCB=45°，则∠ECQ+∠DCB=45°，所以∠HCQ=45°，再证明△HCG≌△HCQ，则得到HG=HQ，然后可计算出.

证明：(1)∵△CDE为等腰直角三角形，∠DCE=90°．

∴CD=CE，∠DCB+∠ECF=90°，

又∵EF⊥BC，

∴∠ECF+∠CEF=90°，

∴∠DCB=∠CEF，

在△DBC和△CEF中， ，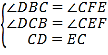

∴△DBC≌△CFE；

（2）解：如图1，

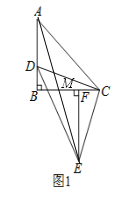
∵△DBC≌△CFE，

∴BD=CF，BC=EF，

∵△ABC为等腰直角三角形，

∴AB=BC，

∴AB=EF，AD=BF，

在△ABM和△EFM中， ，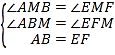

∴△ABM≌△EFM，

∴BM=FM，

∴BF=2BM，

∴AD=2BM，

∴

（3）解：的值不变．

在EH上截取EQ=DG，如图2，

在△CDG和△CEQ中 ，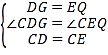

∴△CDG≌△CEQ，

∴CG=CQ，∠DCG=∠ECQ，

∵∠DCG+∠DCB=45°，

∴∠ECQ+∠DCB=45°，

而∠DCE=90°，

∴∠HCQ=45°，

∴∠HCQ=∠HCG，

在△HCG和△HCQ中， ，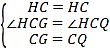

∴△HCG≌△HCQ，

∴HG=HQ，

∴

即式子的值不会发生变化.