Question

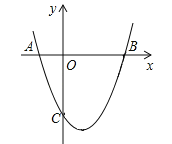
【题目】已知：在平面直角坐标系中，点为坐标原点，的顶点的坐标为，顶点在轴上(点在点的右侧)，点在上，连接，且．

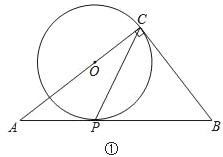
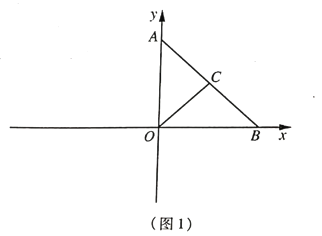
(1)如图1，求点的纵坐标；

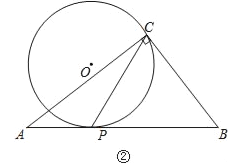
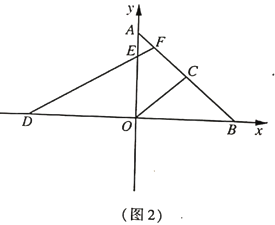
(2)如图2，点在轴上(点在点的左侧)，点在上，连接交于点；若，求证：

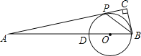
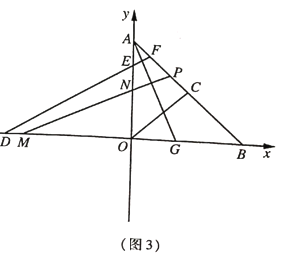
(3)如图3，在(2)的条件下，是的角平分线，点与点关于轴对称，过点作分别交于点，若，求点的坐标．

Answer 1

【答案】（1）点的纵坐标为 2；（2）证明见解析；（3）点的坐标为．

【解析】

（1）由得出，然后通过等量代换得出，则有，进而有，则点C的纵坐标可求；

（2）通过推导出，然后求出，则利用含30°的直角三角形的性质即可证明结论；

（3）连接，过点 作交 轴于点，先推出 ，然后通过垂直和角度之间的代换得出 则有 ，然后进一步，再因为 得出的值，则可求出 ，利用即可求出的值，则点E的坐标可求．

（1）如图 ，过点作于点

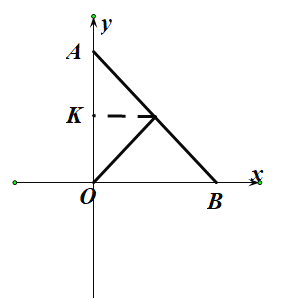
又

∴点的纵坐标为 2．

（2）

又

（3）如图 ，连接，过点作交轴于点

又

∵

∵点与点关于轴对称，点在轴上

∵点在轴上，且在点 的上方．

∴点的坐标为．