题目内容
实数x、y满足 ,求xy的最小值和最大值.
,求xy的最小值和最大值.
解:∵2(x2+y2)≥(x+y)2,
∴2(4a2-2a+2)≥(3a-1)2,
即a2-2a-3≤0,
∴-1≤a≤3;
xy= [(x+y)2-(x2+y2)]=
[(x+y)2-(x2+y2)]= (5a2-4a-1)
(5a2-4a-1)
令f(a)=5a2-4a-1,则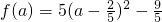 ,
,
故当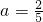 时,f(a)有最小值
时,f(a)有最小值 ,当a=3时有最大值32.
,当a=3时有最大值32.
故xy的最小值为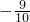 ,最大值为16.
,最大值为16.
分析:根据不等式的性质知:2(x2+y2)≥(x+y)2,据此求出a的取值范围-1≤a≤3;然后再根据完全平方公式求出
xy= [(x+y)2-(x2+y2)]=
[(x+y)2-(x2+y2)]= (5a2-4a-1),令f(a)=5a2-4a-1,这是关于a的二次函数,根据二次函数的单调性求其最值.
(5a2-4a-1),令f(a)=5a2-4a-1,这是关于a的二次函数,根据二次函数的单调性求其最值.
点评:本题考查了一元二次不等式及二次函数的最值.求二次函数的最值时,借助于完全平方公式,将一元二次方程的一般形式转化为顶点式,便于求最值.
∴2(4a2-2a+2)≥(3a-1)2,
即a2-2a-3≤0,
∴-1≤a≤3;
xy=
 [(x+y)2-(x2+y2)]=
[(x+y)2-(x2+y2)]= (5a2-4a-1)
(5a2-4a-1)令f(a)=5a2-4a-1,则
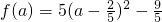 ,
,故当
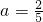 时,f(a)有最小值
时,f(a)有最小值 ,当a=3时有最大值32.
,当a=3时有最大值32.故xy的最小值为
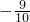 ,最大值为16.
,最大值为16.分析:根据不等式的性质知:2(x2+y2)≥(x+y)2,据此求出a的取值范围-1≤a≤3;然后再根据完全平方公式求出
xy=
 [(x+y)2-(x2+y2)]=
[(x+y)2-(x2+y2)]= (5a2-4a-1),令f(a)=5a2-4a-1,这是关于a的二次函数,根据二次函数的单调性求其最值.
(5a2-4a-1),令f(a)=5a2-4a-1,这是关于a的二次函数,根据二次函数的单调性求其最值.点评:本题考查了一元二次不等式及二次函数的最值.求二次函数的最值时,借助于完全平方公式,将一元二次方程的一般形式转化为顶点式,便于求最值.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 的一元二次方程
的一元二次方程 的两个不相等的实数根
的两个不相等的实数根 、
、 满足
满足 ,求
,求 的值。
的值。 ,求
,求 的值.
的值. .
. 的两个实数根
的两个实数根 、
、 满足
满足 ,求实数m的值.
,求实数m的值. 的一元二次方程
的一元二次方程 的两个不相等的实数根
的两个不相等的实数根 、
、 满足
满足 ,求
,求 的值。
的值。 的一元二次方程
的一元二次方程 的两个不相等的实数根
的两个不相等的实数根 、
、 满足
满足 ,求
,求 的值。
的值。