题目内容
已知正比例函数与反比例函数图象的交点到x轴的距离是3,到y轴的距离是4,求这两个函数的解析式.
解:设正反比例函数的解析式为
设两个函数的图象交点为P(x,y),|x|=4,|y|=3.
当x=4,y=3时,
代入y=k1x,有3=4k1,解得k1= ,
,
∴ ;
;
代入 ,有3=
,有3= ,解得k2=12
,解得k2=12
∴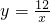 ;
;
当x=-4,y=-3时结果同上;
当x=4,y=-3时代入y=k1x,有-3=4k1,解得k1=- ,
,
∴ ;
;
代入 ,有-3=
,有-3= ,解得k2=-12,
,解得k2=-12,
∴ ;
;
当x=-4,y=3时结果同上.
∴所求函数的解析式为: 和
和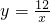 ,
, 和
和 .
.
分析:根据正比例函数与反比例函数图象的交点坐标分4种情况,确定函数式.
点评:本题考查正比例函数的形式以及反比例函数与一次函数的交点问题,注意分类思想的运用.

设两个函数的图象交点为P(x,y),|x|=4,|y|=3.
当x=4,y=3时,
代入y=k1x,有3=4k1,解得k1=
 ,
,∴
 ;
;代入
 ,有3=
,有3= ,解得k2=12
,解得k2=12∴
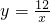 ;
;当x=-4,y=-3时结果同上;
当x=4,y=-3时代入y=k1x,有-3=4k1,解得k1=-
 ,
,∴
 ;
;代入
 ,有-3=
,有-3= ,解得k2=-12,
,解得k2=-12,∴
 ;
;当x=-4,y=3时结果同上.
∴所求函数的解析式为:
 和
和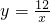 ,
, 和
和 .
.分析:根据正比例函数与反比例函数图象的交点坐标分4种情况,确定函数式.
点评:本题考查正比例函数的形式以及反比例函数与一次函数的交点问题,注意分类思想的运用.

练习册系列答案
相关题目
 例如图.现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
例如图.现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息,解答下列问题:
 成正比例,y2与x2成反比.当x=1时,y=-12;当x=4时,y=7.
成正比例,y2与x2成反比.当x=1时,y=-12;当x=4时,y=7. 时,求y的值.
时,求y的值.