题目内容
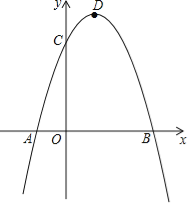
【题目】如图，在函数
（x＞0）的图象上，有点
，
，
，…，
，
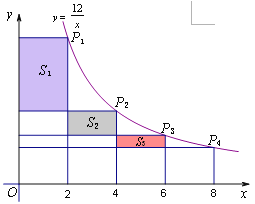
，若的横坐标为a，且以后每点的横坐标与它前面一个点的横坐标的差都为2，过点，，，…，，分别作x轴、y轴的垂线段，构成若干个矩形如图所示，将图中阴影部分的面积从左到右依次记为
，
，
，…，
，则=______，+++…+=__________．（用n的代数式表示）
【答案】6 
【解析】
此题涉及反比例函数的性质，反比例函数
图象上任意一点向x轴,y轴作垂线，与坐标轴围成的矩形面积等于|k|.所以，图中P1点向x轴，y轴作垂线形成的矩形面积等于12.阴影部分面积S1="12-" 矩形下半部分面积，而矩形下半部分也是矩形，其一边长为2，另一边就是P2点的纵坐标，可由P2点求得，从而求得
；+++…+的值，可以考虑将、…平移到左侧与y轴平齐的位置，因为宽度都是2，所以组成一个大矩形，其面积的计算方法与的相似。
解答：
(1)∵P1在
上，
∴S矩形AOBP1=12
∴P2的横坐标为4，代入，得y=3,
∴S矩形COBD=2×3=6
∴= S矩形AOBP1- S矩形COBD=12-6=6
(2)∵P1、P2、P3……的横坐标依次为：2,4,6,…
∴Pn、Pn+1的横坐标为2n 、2n+2
∴参照（1）的计算方法可得：
S1=12-
,
S1+S2=12-
S1+S2+S3=12-…………
∴S1+S2+S3+……+SN=
=
=
练习册系列答案
相关题目
