题目内容
已知函数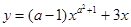 是二次函数,那么a=__________。
是二次函数,那么a=__________。
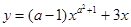 是二次函数,那么a=__________。
是二次函数,那么a=__________。
试题分析:二次函数的定义:形如
 的函数是二次函数.
的函数是二次函数.由题意得
 ,解得
,解得 ,则
,则
点评:本题属于基础应用题,只需学生熟练掌握二次函数的定义,即可完成.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
题目内容
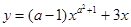 是二次函数,那么a=__________。
是二次函数,那么a=__________。
 的函数是二次函数.
的函数是二次函数. ,解得
,解得 ,则
,则

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案