题目内容
如图,已知直线l经过点A(1,0),与双曲线y=
(x>0)交于点B(2,1).过点P(p,p-1)(p>1)作x轴的平
行线分别交双曲线y=(x>0)和y=-(x<0)于点M、N.
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若
不存在,请说明理由.
解:(1)由点B(2,1)在y=上,有2= ,即m=2。
,即m=2。



设直线l的解析式为 ,由点A(1,0),点B(2,1)在
,由点A(1,0),点B(2,1)在 上,得
上,得 ,,解之,得
,,解之,得
∴所求直线l的解析式为 。
。
(2) 点P(p,p-1)在直线y=2上,∴P在直线l上,是直线y=2和l的交点,见图(1)。
点P(p,p-1)在直线y=2上,∴P在直线l上,是直线y=2和l的交点,见图(1)。
∴根据条件得各点坐标为N(-1,2),M(1,2),P(3,2)。
∴NP=3-(-1)=4,MP=3-1=2,AP= ,
,
BP=
∴在△PMB和△PNA中,∠MPB=∠NPA, 。
。
∴△PMB∽△PNA。
(3)S△AMN= 。下面分情况讨论:
。下面分情况讨论:
?当1<p<3时,延长MP交X轴于Q,见图(2)。设直线MP为 则有
则有



 解得
解得 
则直线MP为

当y=0时,x= ,即点Q的坐标为(
,即点Q的坐标为( ,0)。
,0)。
则 ,
,
由2=4 有
有 ,解之,p=3(不合,舍去),p=
,解之,p=3(不合,舍去),p= 。
。
?当p=3时,见图(1)S△AMP= =S△AMN。不合题意。
=S△AMN。不合题意。
?当p>3时,延长PM交X轴于Q,见图(3)。
此时,S△AMP大于情况?当p=3时的三角形面积S△AMN。故不存在实数p,使得S△AMN=4S△AMP。
综上,当p= 时,S△AMN=4S△AMP。解析:
时,S△AMN=4S△AMP。解析:
略
 ,即m=2。
,即m=2。


|
 ,由点A(1,0),点B(2,1)在
,由点A(1,0),点B(2,1)在 上,得
上,得 ,,解之,得
,,解之,得
∴所求直线l的解析式为
 。
。(2)
 点P(p,p-1)在直线y=2上,∴P在直线l上,是直线y=2和l的交点,见图(1)。
点P(p,p-1)在直线y=2上,∴P在直线l上,是直线y=2和l的交点,见图(1)。∴根据条件得各点坐标为N(-1,2),M(1,2),P(3,2)。
∴NP=3-(-1)=4,MP=3-1=2,AP=
 ,
,BP=

∴在△PMB和△PNA中,∠MPB=∠NPA,
 。
。∴△PMB∽△PNA。
(3)S△AMN=
 。下面分情况讨论:
。下面分情况讨论:?当1<p<3时,延长MP交X轴于Q,见图(2)。设直线MP为
 则有
则有


 解得
解得 
则直线MP为


当y=0时,x=
 ,即点Q的坐标为(
,即点Q的坐标为( ,0)。
,0)。 则
 ,
,由2=4
 有
有 ,解之,p=3(不合,舍去),p=
,解之,p=3(不合,舍去),p= 。
。?当p=3时,见图(1)S△AMP=
 =S△AMN。不合题意。
=S△AMN。不合题意。?当p>3时,延长PM交X轴于Q,见图(3)。
此时,S△AMP大于情况?当p=3时的三角形面积S△AMN。故不存在实数p,使得S△AMN=4S△AMP。
综上,当p=
 时,S△AMN=4S△AMP。解析:
时,S△AMN=4S△AMP。解析:略

练习册系列答案
相关题目


 )作x轴的平行线分别交双曲线y=
)作x轴的平行线分别交双曲线y=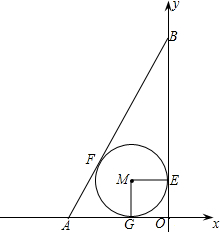 如图,已知直线l经过点D(-1,4),与x轴的负半轴和y轴的正半轴分别交于A,B两点,且直角△AOB的内切圆的面积为π,求直线l对应的一次函数的表达式.
如图,已知直线l经过点D(-1,4),与x轴的负半轴和y轴的正半轴分别交于A,B两点,且直角△AOB的内切圆的面积为π,求直线l对应的一次函数的表达式. (2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=
(2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=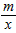 (x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交双曲线y=
(x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交双曲线y=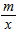 (x>0)和y=-
(x>0)和y=-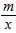 (x<0)于点M、N。
(x<0)于点M、N。
 经过点
经过点 和点
和点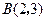 ,另一条直线
,另一条直线

 ,且与
,且与 轴相交于点
轴相交于点 .
. 的面积为3,求
的面积为3,求 的值.
的值.