题目内容
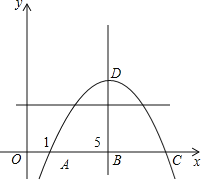
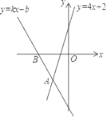
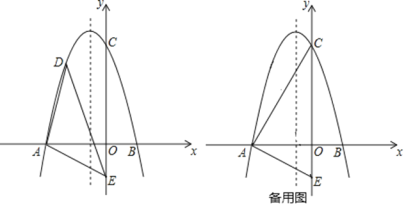
【题目】如图所示,在平面直角坐标系中,二次函数![]() 交x轴于
交x轴于![]() ,
,![]() ,在y轴上有一点
,在y轴上有一点![]() ,连接AE.
,连接AE.
![]() 求二次函数的表达式;
求二次函数的表达式;
![]() 点D是第二象限内的抛物线上一动点.
点D是第二象限内的抛物线上一动点.
①求![]() 面积最大值并写出此时点D的坐标;
面积最大值并写出此时点D的坐标;
②若![]() ,求此时点D坐标;
,求此时点D坐标;
【答案】(1)![]() ;(2)①D(
;(2)①D(![]() ,
,![]() );
);![]() ;②
;②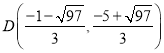
【解析】
(1)将A(4,0),B(2,0)代入y=ax2+bx+6(a≠0),求得![]() ;
;
(2)①由已知可求:![]() ,AE的直线解析式
,AE的直线解析式![]() ,设
,设![]() ,过点D与AE垂直的直线解析式为
,过点D与AE垂直的直线解析式为![]() ,两直线的交点为
,两直线的交点为![]() ,可求
,可求![]() ,则有当
,则有当![]() 时,DQ最大为
时,DQ最大为![]() ,则面积最大值为
,则面积最大值为![]() ;
;
②过点A作AN⊥DE,DE与x中交于点F,由tan∠AED=![]() ,可求AN=
,可求AN=![]() ,NE=3
,NE=3![]() ,因为Rt△AFN∽Rt△EFO,
,因为Rt△AFN∽Rt△EFO,![]() ,则有
,则有![]() ,所以F(2,0),得到EF直线解析式为y=x2,直线与抛物线的交点为D点.
,所以F(2,0),得到EF直线解析式为y=x2,直线与抛物线的交点为D点.
解:![]() 将
将![]() ,
,![]() 代入
代入![]() ,
,
可得![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() ,AE的直线解析式
,AE的直线解析式![]() ,
,
设![]() ,
,
过点D与AE垂直的直线解析式为![]() ,
,
两直线的交点为![]() ,
,
![]() ,
,
当![]() 时,DQ最大为
时,DQ最大为![]() ,
,
![]() ;
;
![]() 过点A作
过点A作![]() ,DE与x轴交于点F,
,DE与x轴交于点F,
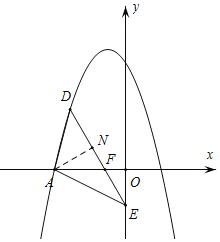
![]() ,
,
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线解析式为
直线解析式为![]() ,
,
![]() 时,
时,![]() ,
,
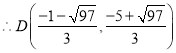 ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目