题目内容
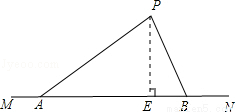
(本题满分10分)如图,海岸线MN上有A,B两艘船,均收到已触角搁浅的船P求救信号﹒经测量,∠PAB=37°, ∠PBA=67°,AB的距离为42海里﹒

(1)求船P到海岸线MN的距离;
(2)若船A,船B分别以20海里/时,15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断那艘船先到达船P处﹒
(参考数据:sin67°≈ ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,Sin37°≈
,Sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
(1)PE=24海里;
(2)B船先到达P处.
【解析】
试题分析:(1)过点P作PE⊥AB于点E,在Rt△APE和Rt△BPE中解出PE即可;
(2)在Rt△BPF中,求出BP,分别计算出两艘船需要的时间,即可作出判断
试题解析:(1)如图:过点P作PE⊥AB于点E,
在Rt△APE中,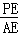 =tan37°,
=tan37°,
AE=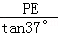 ;
;
在Rt△BPE中,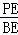 =tan67°,
=tan67°,
BE=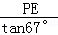 ;
;
∴AE+EB=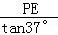 +
+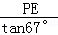 =42,
=42,
∴ +
+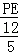 ≈42,
≈42,
∴(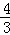 +
+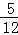 )PE≈42,
)PE≈42,
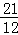 PE≈42,
PE≈42,
PE≈42×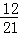 =24.
=24.
(2)在Rt△APE中,sin37°=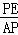 ,
,
∴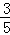 ≈
≈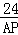 ,
,
解得AP≈40海里;
A船所用时间为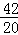 =
=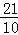 小时;
小时;
在Rt△BPE中,sin67°=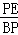 ,
,
∴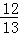 ≈
≈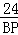 ,
,
解得BP≈26海里;
B船所用时间为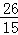 小时;
小时;
∴B船先到达P处.
考点:解直角三角形的应用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
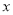 元(
元(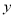 元.
元.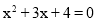 的根的情况是( )
的根的情况是( ) ,其中x是方程
,其中x是方程 的根﹒
的根﹒