题目内容
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=![]() x2+bx+c经过点B,且顶点在直线x=
x2+bx+c经过点B,且顶点在直线x=![]() 上.
上.

(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
解析:
|
分析:(1)根据抛物线y= (2)根据菱形的性质得出C、D两点的坐标分别是(5,4)、(2,0),利用图象上点的性质得出x=5或2时,y的值即可. (3)首先设直线CD对应的函数关系式为y=kx+b,求出解析式,当x= (4)利用MN∥BD,得出△OMN∽△OBD,进而得出 解答:解:(1)∵抛物线y= ∴c=4, ∵顶点在直线x= ∴ ∴所求函数关系式为 (2)在Rt△ABO中,OA=3,OB=4, ∴AB= ∵四边形ABCD是菱形, ∴BC=CD=DA=AB=5, ∴C、D两点的坐标分别是(5,4)、(2,0), 当x=5时,y= 当x=2时,y= ∴点C和点D都在所求抛物线上; (3)设CD与对称轴交于点P,则P为所求的点, 设直线CD对应的函数关系式为y=kx+b, 则 解得: ∴ 当x= ∴P( (4)∵MN∥BD, ∴△OMN∽△OBD, ∴ 设对称轴交x于点F, 则 ∵ S= =- S存在最大值. 由S=- ∴当S= 此时,点M的坐标为(0,
点评:此题主要考查了二次函数的综合应用,以及菱形性质和待定系数法求解析式,求图形面积最值,利用二次函数的最值求出是解题关键. |
提示:
|
考点:二次函数综合题. |

 ,
,
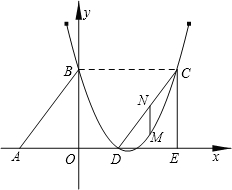 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 象在第四象限的交点,AB⊥x轴于B,且S△ABO=
象在第四象限的交点,AB⊥x轴于B,且S△ABO= 标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=