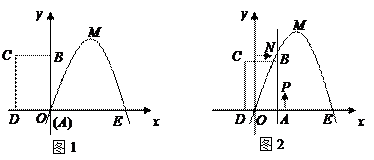题目内容
如图12,已知抛物线![]() 交
交![]() 轴于A、B两点,交
轴于A、B两点,交![]() 轴于点C,抛物线的对称轴交
轴于点C,抛物线的对称轴交![]() 轴于点E,点B的坐标为(
轴于点E,点B的坐标为(![]() ,0).
,0).
(1)求抛物线的对称轴及点A的坐标;
(2)在平面直角坐标系![]() 中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
(3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
 |
解:(1)① 对称轴![]() ······················· 2分
······················· 2分
② 当![]() 时,有
时,有![]()
解之,得 ![]() ,
,![]()
∴ 点A的坐标为(![]()
![]() ,0).····················· 4分
,0).····················· 4分
(2)满足条件的点P有3个,分别为(![]() ,3),(2,3),(
,3),(2,3),(![]() ,
,![]() ).···· 7分
).···· 7分
(3)存在.······························ 8分
当![]() 时,
时,![]() ∴ 点C的坐标为(0,3)
∴ 点C的坐标为(0,3)
∵ DE∥![]() 轴,AO
轴,AO![]() 3,EO
3,EO![]() 2,AE
2,AE![]() 1,CO
1,CO![]() 3
3
∴ ![]() ∽
∽![]() ∴
∴ ![]() 即
即 ![]() ∴ DE
∴ DE![]() 1····· 9分
1····· 9分
∴ ![]()
![]()
![]() 4
4
在OE上找点F,使OF![]()
![]() ,此时
,此时![]()
![]()
![]() 2,直线CF把四边形DEOC
2,直线CF把四边形DEOC
分成面积相等的两部分,交抛物线于点M.·················· 10分
![]() 设直线CM的解析式为
设直线CM的解析式为![]() ,它经过点
,它经过点![]() .
.
则![]() ···························· 11分
···························· 11分
解之,得 ![]() ∴ 直线CM的解析式为
∴ 直线CM的解析式为 ![]() ·········· 12分
·········· 12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

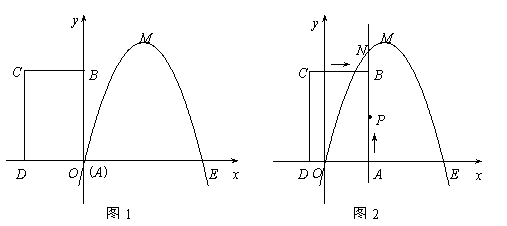
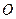 和
和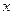 轴上另一点
轴上另一点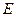 ,顶点
,顶点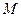 的坐标为
的坐标为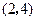 ;矩形
;矩形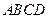 的顶点
的顶点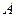 与点
与点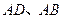 分别在
分别在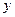 轴上,且
轴上,且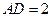 ,
,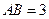 .
. 也以相同的速度从点
也以相同的速度从点 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为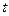 秒(
秒(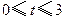 ),直线
),直线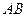 与该抛物线的交点为
与该抛物线的交点为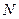 (如图2所示).
(如图2所示).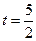 时,判断点
时,判断点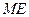 上,并说明理由;
上,并说明理由;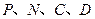 为顶点的多边形面积为
为顶点的多边形面积为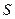 ,试问
,试问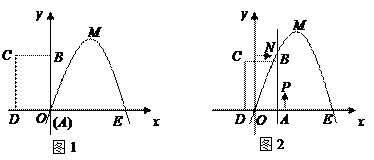
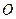 和
和 轴上另一点
轴上另一点 ,顶点
,顶点 的坐标为
的坐标为 ;矩形
;矩形 的顶点
的顶点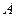 与点
与点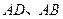 分别在
分别在 轴上,且
轴上,且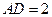 ,
, .
.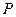 也以相同的速度从点
也以相同的速度从点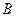 匀速移动.设它们运动的时间为
匀速移动.设它们运动的时间为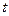 秒(
秒(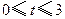 ),直线
),直线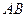 与该抛物线的交点为
与该抛物线的交点为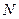 (如图2所示).
(如图2所示).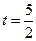 时,判断点
时,判断点 上,并说明理由;
上,并说明理由;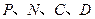 为顶点的多边形面积为
为顶点的多边形面积为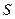 ,试问
,试问