Question

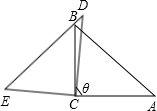在△ABC中，已知∠ACB=90°，∠A=40°．若以点C为中心，将△ABC旋转θ角到△DEC的位置，使B点恰好落在边DE上（如图所示）．则θ=________°．

Answer 1

80
分析：由△ABC以点C为中心旋转θ角到△DEC，且B点恰好落在边DE上，根据旋转的性质得到∠ECB=∠ACD=θ，CE=CB，∠E=∠ABC，而∠ACB=90°，∠A=40°，根据三角形的内角和定理可得到∠ABC=90°-40°=50°，∠ECB=θ=180°-50°-50°=80°．
解答：∵△ABC以点C为中心旋转θ角到△DEC，且B点恰好落在边DE上，
∴∠ECB=∠ACD=θ，CE=CB，∠E=∠ABC，
而∠ACB=90°，∠A=40°，
∴∠ABC=90°-40°=50°，
∴∠E=50°，
而CE=CB，
∴∠E=∠EBC=50°，
∴∠ECB=θ=180°-50°-50°=80°．
故答案为：80°．
点评：本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．也考查了等腰三角形的性质和三角形的内角和定理．