题目内容
梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD+BC=26,求梯形ABCD的高.分析:作DE∥AC交BC的延长线于点E,作DF⊥BC于F,先证明四边形ACED是平行四边形,可推出AC=DE,根据已知条件得出∠BDE=90°,然后即可得出答案.
解答: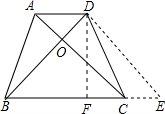 解:作DE∥AC交BC的延长线于点E,作DF⊥BC于F,
解:作DE∥AC交BC的延长线于点E,作DF⊥BC于F,
∵DE∥AC,AD∥BC,
∴四边形ACED是平行四边形.
∴AC=DE,
∵AC=BD,
∴BD=DE,
∵AC⊥BD,
∴∠BDE=90°,
DF=
BE=
(BC+CE)=
(AD+BC)=13,
故梯形ABCD的高为13.
 解:作DE∥AC交BC的延长线于点E,作DF⊥BC于F,
解:作DE∥AC交BC的延长线于点E,作DF⊥BC于F,∵DE∥AC,AD∥BC,
∴四边形ACED是平行四边形.
∴AC=DE,
∵AC=BD,
∴BD=DE,
∵AC⊥BD,
∴∠BDE=90°,
DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故梯形ABCD的高为13.
点评:本题考查了梯形的知识,难度一般,关键是正确地作出辅助线进行求解.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
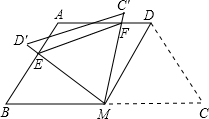 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点. DE.
DE. 如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.
如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.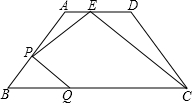 如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是
如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是 分别交边CD、BC于点F、E,若AD=3,BC=12,
分别交边CD、BC于点F、E,若AD=3,BC=12,