题目内容
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于 点F.
点F.
问:(1)图中△APD与哪个三角形全等?试证明之;
(2)△APE与哪个三角形相似?试证明之;
(3)如果PE=4,EF=5,求线段PC的长.
解:(1)△APD≌△CPD,
∵四边形ABCD是菱形,
∴CD=DA,∠CDP=∠ADP,DP公共.
∴△APD≌△CPD.
(2)△APE∽△FPA.
∵根据(1)的结论知道∠DCP=∠DAP,而CD∥AF,
∴∠F=∠DAP,
由(1)△APD≌△CPD,可得∠DCR=∠DAP,
∴∠F=∠DCP,
∴APE∽△FPA.
(3)根据(1),(2)可以得到 .
.
分析:(1)△APD与△CPD全等.根据菱形的性质可以找到全等条件;
(2)△APE∽△FPA,根据(1)的结论知道∠DCP=∠DAP,而根据CD∥AF得到∠F=∠DAP,这样就可以证明它们相似;(3)根据(1),(2)可以得到 .
.
点评:此题主要考查了菱形、相似三角形和全等三角形的性质与判定.
∵四边形ABCD是菱形,
∴CD=DA,∠CDP=∠ADP,DP公共.
∴△APD≌△CPD.
(2)△APE∽△FPA.
∵根据(1)的结论知道∠DCP=∠DAP,而CD∥AF,
∴∠F=∠DAP,
由(1)△APD≌△CPD,可得∠DCR=∠DAP,
∴∠F=∠DCP,
∴APE∽△FPA.
(3)根据(1),(2)可以得到
 .
.分析:(1)△APD与△CPD全等.根据菱形的性质可以找到全等条件;
(2)△APE∽△FPA,根据(1)的结论知道∠DCP=∠DAP,而根据CD∥AF得到∠F=∠DAP,这样就可以证明它们相似;(3)根据(1),(2)可以得到
 .
.点评:此题主要考查了菱形、相似三角形和全等三角形的性质与判定.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
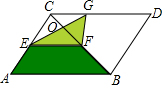 如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.
如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.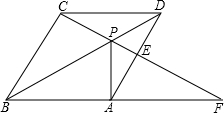 长线于F.
长线于F. (2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.
(2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.
