Question

【题目】已知在等腰△ABC中，AB=AC=，BC=4，点D从A出发以每秒个单位的速度向点B运动，同时点E从点B出发以每秒4个单位的速度向点C运动，在DE的右侧作∠DEF=∠B，交直线AC于点F，设运动的时间为t秒，则当△ADF是一个以AD为腰的等腰三角形时，t的值为_____．

Answer 1

【答案】

【解析】

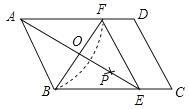
当△ADF是一个以AD为腰的等腰三角形时，如图2，只能AD＝AF，由题意DF＝4t，BE＝4t，DF∥BE，推出四边形BEFD是平行四边形，由△ABC∽△BED，可得，延长构建方程即可解决问题；

如图1，过A作AG⊥BC于G，

∵AB＝AC＝，

∴BG＝CG＝2，

由勾股定理得：AG＝＝1，

由图形可知：∠BAC是钝角，

∴当△ADF是一个以AD为腰的等腰三角形时，如图2，只能AD＝AF，

由题意DF＝4t，BE＝4t，DF∥BE，

∴四边形BEFD是平行四边形，

∴∴DEF＝∠BDE＝∠B，

∴△ABC∽△BED，

∴，

∴，

∴t＝，

故答案为：．