ĢāÄæÄŚČŻ
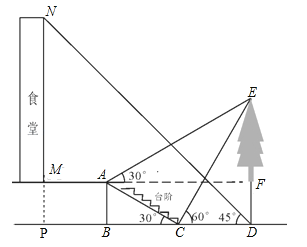
”¾ĢāÄæ”抔Ć÷ĻėŅŖ²āĮæѧŠ£Ź³ĢĆŗĶŹ³ĢĆÕżĒ°·½Ņ»æĆŹ÷µÄøß¶Č£¬Ėū“ÓŹ³ĢĆĀ„µ×M“¦³ö·¢£¬ĻņĒ°×ß3Ć×µ½“ļA“¦£¬²āµĆŹ÷¶„¶ĖEµÄŃö½ĒĪŖ30”ć£¬ĖūÓÖ¼ĢŠų×ßĻĀĢؽ׵½“ļC“¦£¬²āµĆŹ÷µÄ¶„¶ĖEµÄŃö½ĒŹĒ60”ć£¬ŌŁ¼ĢŠųĻņĒ°×ßµ½“óŹ÷µ×D“¦£¬²āµĆŹ³ĢĆĀ„¶„NµÄŃö½ĒĪŖ45”ć£®ŅŃÖŖAµćĄėµŲĆęµÄø߶ČAB=2Ć×£¬”ĻBCA=30”ć£¬ĒŅB”¢C”¢DČżµćŌŚĶ¬Ņ»Ö±ĻßÉĻ£®
£Ø1£©ĒóŹ÷DEµÄøß¶Č£»
£Ø2£©ĒóŹ³ĢĆMNµÄøß¶Č£®

”¾“š°ø”æ£Ø1£©6£»£Ø2£©![]() £®
£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÉčDE=x£¬æɵĆEF=DE©DF=x©2£¬“Ó¶ųµĆAF=![]() £Øx©2£©£¬ŌŁĒó³öCD=
£Øx©2£©£¬ŌŁĒó³öCD=![]() x”¢BCµÄ³¤£¬øł¾ŻAF=BDæÉµĆ¹ŲÓŚxµÄ·½³Ģ£¬½āÖ®æÉµĆ£»
x”¢BCµÄ³¤£¬øł¾ŻAF=BDæÉµĆ¹ŲÓŚxµÄ·½³Ģ£¬½āÖ®æÉµĆ£»
£Ø2£©ŃÓ³¤NM½»DBŃÓ³¤ĻßÓŚµćP£¬ÖŖAM=BP=3£¬ÓÉ£Ø1£©µĆCD=![]() x=
x=![]() ӢBC=
”¢BC=![]() £¬øł¾ŻNP=PDĒŅAB=MPæɵƓš°ø£®
£¬øł¾ŻNP=PDĒŅAB=MPæɵƓš°ø£®
ŹŌĢā½āĪö£ŗ£Ø1£©ČēĶ¼£¬ÉčDE=x£¬”ßAB=DF=2£¬”ąEF=DE©DF=x©2£¬”ß”ĻEAF=30”ć£¬”ąAF=![]() =
=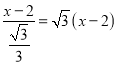 £¬ÓÖ”ßCD=
£¬ÓÖ”ßCD=![]() =
=![]() =
=![]() x£¬BC=
x£¬BC=![]() =
=![]() =
=![]() £¬”ąBD=BC+CD=
£¬”ąBD=BC+CD=![]() +
+![]() x£¬ÓÉAF=BDæɵĆ
x£¬ÓÉAF=BDæɵĆ![]() £Øx©2£©=
£Øx©2£©=![]() +
+![]() x£¬½āµĆ£ŗx=6£¬”ąŹ÷DEµÄø߶ČĪŖ6Ć×£»
x£¬½āµĆ£ŗx=6£¬”ąŹ÷DEµÄø߶ČĪŖ6Ć×£»
£Ø2£©ŃÓ³¤NM½»DBŃÓ³¤ĻßÓŚµćP£¬ŌņAM=BP=3£¬ÓÉ£Ø1£©ÖŖCD=![]() x=
x=![]() ”Į6=
”Į6=![]() £¬BC=
£¬BC=![]() £¬”ąPD=BP+BC+CD=3+
£¬”ąPD=BP+BC+CD=3+![]() +
+![]() =3+
=3+![]() £¬”ß”ĻNDP=45”ć£¬ĒŅMP=AB=2£¬”ąNP=PD=3+
£¬”ß”ĻNDP=45”ć£¬ĒŅMP=AB=2£¬”ąNP=PD=3+![]() £¬”ąNM=NP©MP=3+
£¬”ąNM=NP©MP=3+![]() ©2=
©2=![]() £¬”ąŹ³ĢĆMNµÄø߶ČĪŖ
£¬”ąŹ³ĢĆMNµÄø߶ČĪŖ![]() Ć×£®
Ć×£®