题目内容
在△ABC中，∠ACB=90°，AC=6，BC=8，D为AB的中点，则CD=________．
5
分析：先运用勾股定理求出斜边AB的长度，再根据直角三角形斜边上的中线等于斜边的一半即可得出CD的长．
解答：
解：如图，∵在△ABC中，∠ACB=90°，AC=6，BC=8，
∴AB=
=10，
又∵D为AB的中点，
∴CD=
AB=5．
故答案是：5．
点评：本题考查了勾股定理及直角三角形斜边上的中线等于斜边的一半的性质，比较简单．
分析：先运用勾股定理求出斜边AB的长度，再根据直角三角形斜边上的中线等于斜边的一半即可得出CD的长．
解答：
解：如图，∵在△ABC中，∠ACB=90°，AC=6，BC=8，∴AB=
=10，又∵D为AB的中点，
∴CD=
AB=5．故答案是：5．
点评：本题考查了勾股定理及直角三角形斜边上的中线等于斜边的一半的性质，比较简单．
练习册系列答案
相关题目
在△ABC中，AC=8，BC=6，AB=10，则△ABC的外接圆半径长为（ ）
| A、10 | B、5 | C、6 | D、4 |
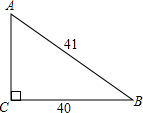如图，在△ABC中，AC=
如图所示，在△ABC中，AC与⊙O相切于点A，AC=AB=2，⊙O交BC于D．
（2013•松江区二模）如图，已知在△ABC中，AC=15，AB=25，sin∠CAB=