题目内容
等腰梯形的两底长度和为26cm，当两条对角线互相垂直时，则梯形的面积是________．
169
分析：因为两条对角线互相垂直，所以对角线和两个底边组成等腰直角三角形，所以可求出梯形的高，进而求出梯形的面积．
解答：
解：作EF⊥AD交AD，BC于E，F．
∵四边形ABCD是等腰梯形，AC⊥BD，
∴OE=
AD，OF=BC，
∴EF=×26=13．
∴梯形的面积为：×26×13=169．
故答案为：169．
点评：本题考查等腰梯形的性质，关键知道对角线互相垂直时，对角线和底边组成的是等腰直角三角形．
分析：因为两条对角线互相垂直，所以对角线和两个底边组成等腰直角三角形，所以可求出梯形的高，进而求出梯形的面积．
解答：
解：作EF⊥AD交AD，BC于E，F．∵四边形ABCD是等腰梯形，AC⊥BD，
∴OE=
AD，OF=BC，∴EF=
×26=13．∴梯形的面积为：
×26×13=169．故答案为：169．
点评：本题考查等腰梯形的性质，关键知道对角线互相垂直时，对角线和底边组成的是等腰直角三角形．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
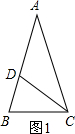
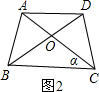
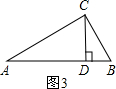
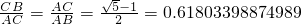．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．
