Question

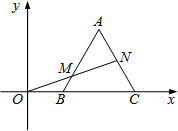如图，平面直角坐标系内，正三角形ABC的顶点B，C的坐标分别为（1，0），（3，0），过坐标原点O的一条直线分别与边AB，AC交于点M，N，若OM=MN，则点M的坐标为________．

Answer 1

分析：从OM=MN结合点B和点C的坐标求得AN等于1，并结合等边三角形ABC点B和点C的坐标，从而求得点M坐标．
解答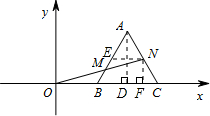：解：∵B（1，0），C（3，0），
∴OB=1，OC=3，
∴BC=2，
过点N作EN∥OC交AB于E，过点A作AD⊥BC于D，NF⊥BC于F，
∴∠ENM=∠BOM，
∵OM=NM，∠EMN=∠BMO，
∴△ENM≌△BOM，
∴EN=OB=1，
∵△ABC是正三角形，
∴AD=，BD=BC=1，
∴OD=2，
∴A（2，），
∴△AEN也是正三角形，
∴AN=EN=1，
∴AN=CN，
∴，
∴．
故答案为：．
点评：本题考查等边三角形的性质，OM=MN，得到线段关系解得AN得1，进而求得．