题目内容
试一试,你一定能成功哟!
已知:正方形的边长为1.
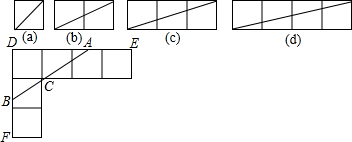
(1)如图(a),可以计算出正方形的对角线长为
.如图(b),求两个并排成的矩形的对角线的长.n个呢?
(2)若把(c)(d)两图拼成如下“L”形如图,过C作直线交DE于A,交DF于B.若DB=
,求DA的长度.
已知:正方形的边长为1.
(1)如图(a),可以计算出正方形的对角线长为
| 2 |
(2)若把(c)(d)两图拼成如下“L”形如图,过C作直线交DE于A,交DF于B.若DB=
| 5 |
| 3 |

考点:勾股定理,作图—应用与设计作图
专题:
分析:(1)根据前面几个图形及正方形的边长为1,利用勾股定理可得出答案;根据以上规律可得出n个正方形并排成的矩形的对角线长;
(2)利用相似三角形的性质求出AN,即可得出AD的长.
(2)利用相似三角形的性质求出AN,即可得出AD的长.
解答:解:(1)利用勾股定理可得:
可以计算出正方形的对角线长为
;
两个正方形并排成的矩形的对角线的长为
;
三个正方形并排成的矩形的对角线的长为
四个正方形并排成的矩形的对角线的长为
;
…
根据以上规律,n个正方形并排成的矩形的对角线长为
;
(2)过点B作BF⊥NC于点F,
由题意可得出:△ANC∽△BFC,
∴
=
,
∴
=
,
解得:AN=
,
∴AD=1+
=
.
可以计算出正方形的对角线长为
| 2 |
两个正方形并排成的矩形的对角线的长为
| 5 |
三个正方形并排成的矩形的对角线的长为
| 10 |
四个正方形并排成的矩形的对角线的长为
| 17 |
…
根据以上规律,n个正方形并排成的矩形的对角线长为
| n2+1 |
(2)过点B作BF⊥NC于点F,
由题意可得出:△ANC∽△BFC,
∴
| CF |
| NC |
| BF |
| AN |
∴
| ||
| 1 |
| 1 |
| AN |
解得:AN=
| 3 |
| 2 |
∴AD=1+
| 3 |
| 2 |
| 5 |
| 2 |
点评:此题考查了勾股定理的知识以及相似三角形的判定与性质和规律性问题,关键是得出△ANC∽△BFC.

练习册系列答案
相关题目
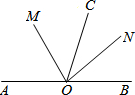 已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由.
已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由. 如图,∠B=30°,∠C=70°,则∠CAD=
如图,∠B=30°,∠C=70°,则∠CAD=