题目内容
经过点(2, )的双曲线
)的双曲线 一定经过点
一定经过点
- A.(
 ,2)
,2) - B.(-2,
 )
) - C.(-2,
 )
) - D.(
 ,-2)
,-2)
C
分析:根据反比例函数中k=xy的特点求出k的值,再把各选项进行一、一检验即可.
解答:∵点(2, )在双曲线
)在双曲线 上,
上,
∴k=2×(- )=-2
)=-2 ,
,
A、∵2× =2
=2 ≠-2
≠-2 ,∴此点不在反比例函数的图象上,故本选项错误;
,∴此点不在反比例函数的图象上,故本选项错误;
B、∵(-2)×(- )=2
)=2 ≠-2
≠-2 ,∴此点不在反比例函数的图象上,故本选项错误;
,∴此点不在反比例函数的图象上,故本选项错误;
C、∵(-2)× =-2
=-2 ,∴此点在反比例函数的图象上,故本选项正确;
,∴此点在反比例函数的图象上,故本选项正确;
D、∵(- )×(-2)=2
)×(-2)=2 ≠-2
≠-2 ,∴此点不在反比例函数的图象上,故本选项错误.
,∴此点不在反比例函数的图象上,故本选项错误.
故选C.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中k=xy的特点是解答此题的关键.
分析:根据反比例函数中k=xy的特点求出k的值,再把各选项进行一、一检验即可.
解答:∵点(2,
 )在双曲线
)在双曲线 上,
上,∴k=2×(-
 )=-2
)=-2 ,
,A、∵2×
 =2
=2 ≠-2
≠-2 ,∴此点不在反比例函数的图象上,故本选项错误;
,∴此点不在反比例函数的图象上,故本选项错误;B、∵(-2)×(-
 )=2
)=2 ≠-2
≠-2 ,∴此点不在反比例函数的图象上,故本选项错误;
,∴此点不在反比例函数的图象上,故本选项错误;C、∵(-2)×
 =-2
=-2 ,∴此点在反比例函数的图象上,故本选项正确;
,∴此点在反比例函数的图象上,故本选项正确;D、∵(-
 )×(-2)=2
)×(-2)=2 ≠-2
≠-2 ,∴此点不在反比例函数的图象上,故本选项错误.
,∴此点不在反比例函数的图象上,故本选项错误.故选C.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中k=xy的特点是解答此题的关键.

练习册系列答案
相关题目
 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC上的中线BD的反向延长线交y轴负半轴于点E,双曲y=
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC上的中线BD的反向延长线交y轴负半轴于点E,双曲y= 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC上的中线BD的反向延长线交y轴负半轴于点E,双曲y=
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC上的中线BD的反向延长线交y轴负半轴于点E,双曲y=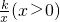 的图象经过点A,S△EBC=6,则k=________.
的图象经过点A,S△EBC=6,则k=________.