题目内容
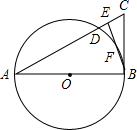 如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=
如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=| 1 |
| 2 |
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC=
| 1 |
| 4 |
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)首先连接AF,由AB为直径,根据圆周角定理,可得∠AFB=90°,又由AE=AB,∠EBC=
∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;
(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.
| 1 |
| 2 |
(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.
解答: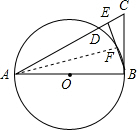 (1)证明:连接AF.
(1)证明:连接AF.
∵AB为直径,
∴∠AFB=90°.
∵AE=AB,
∴△ABE为等腰三角形.
∴∠BAF=
∠BAC.
∵∠EBC=
∠BAC,
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°.
∴∠ABC=90°.
即AB⊥BC,
∴BC与⊙O相切.
(2)解:过E作EG⊥BC于点G,
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC=
.
在△AFB中,∠AFB=90°,
∵AB=8,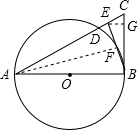
∴BF=AB•sin∠BAF=8×
=2,
∴BE=2BF=4.
在△EGB中,∠EGB=90°,
∴EG=BE•sin∠EBC=4×
=1,
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴
=
.
∴
=
,
∴CE=
,
∴AC=AE+CE=8+
=
.
 (1)证明:连接AF.
(1)证明:连接AF.∵AB为直径,
∴∠AFB=90°.
∵AE=AB,
∴△ABE为等腰三角形.
∴∠BAF=
| 1 |
| 2 |
∵∠EBC=
| 1 |
| 2 |
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°.
∴∠ABC=90°.
即AB⊥BC,
∴BC与⊙O相切.
(2)解:过E作EG⊥BC于点G,
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC=
| 1 |
| 4 |
在△AFB中,∠AFB=90°,
∵AB=8,

∴BF=AB•sin∠BAF=8×
| 1 |
| 4 |
∴BE=2BF=4.
在△EGB中,∠EGB=90°,
∴EG=BE•sin∠EBC=4×
| 1 |
| 4 |
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴
| CE |
| CA |
| EG |
| AB |
∴
| CE |
| CE+8 |
| 1 |
| 8 |
∴CE=
| 8 |
| 7 |
∴AC=AE+CE=8+
| 8 |
| 7 |
| 64 |
| 7 |
点评:此题考查了切线的判定、相似三角形的判定与性质、圆周角定理、等腰三角形的性质以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 北京时间2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线
北京时间2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震,空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线 已知:如图,在△ABC中,∠ABC=90°.DC⊥AC于点C,且CD=CA,DE⊥BC交BC的延长线于点E.
已知:如图,在△ABC中,∠ABC=90°.DC⊥AC于点C,且CD=CA,DE⊥BC交BC的延长线于点E.
 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则
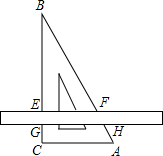 如图,将直尺垂直三角板ABC的直角边BC放置,直尺的一边被三角板截出的边长EF=
如图,将直尺垂直三角板ABC的直角边BC放置,直尺的一边被三角板截出的边长EF=