题目内容
如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 同时出发,沿
同时出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动.当点
运动.当点![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点同时停止运动.以
两点同时停止运动.以![]() 为一边向上作正方形
为一边向上作正方形![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() ,正方形
,正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() .
.
(1)当![]() _____s时,点
_____s时,点![]() 与点
与点![]() 重合;
重合;
(2)当![]() _____s时,点
_____s时,点![]() 在
在![]() 上;
上;
(3)当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,求
两点)时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.

[答案] (1) 1; (2) ![]() . (3)
. (3)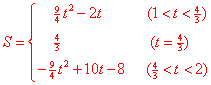 .
.
[考点] 动点问题,一次函数、二次函数综合运用,数学分类讨论思想.
[解析] (1) 因为动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 同时出发,沿
同时出发,沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 运动.
运动.![]() ,
,![]() 同时出发,运动速度都是
同时出发,运动速度都是![]() ,所以
,所以![]() ,
,![]() 运动到
运动到![]() 的中点时重合,
的中点时重合,![]() ,
,![]() ,此时
,此时![]() .
.
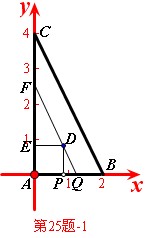 (2) 如图(第25题-1),以
(2) 如图(第25题-1),以![]() 为直角坐标系的原点,
为直角坐标系的原点,![]() 方向为
方向为![]() 轴的正方向,
轴的正方向,![]() 方向为
方向为![]() 轴的正方向,建立直角坐标系,则
轴的正方向,建立直角坐标系,则![]() 、
、![]() 、
、![]() .
.
设![]() 时刻时,点
时刻时,点![]() 在
在![]() 上,因为正方形
上,因为正方形![]() ,所以
,所以![]() 、
、![]() 、
、![]() 、又在
、又在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,得过
,得过![]() 、
、![]() 的一次函数的解析式为:
的一次函数的解析式为:![]() ,由
,由![]() 在
在![]() 上,所以
上,所以![]() 的坐标满足
的坐标满足![]() 的解析式,即:
的解析式,即:![]() .
.
(3)因为由(1)知![]() ,
,![]() 在
在![]() 时相遇,所以,只有当
时相遇,所以,只有当![]() 时,点
时,点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点),正方形
两点),正方形![]() 和梯形
和梯形![]() 重合部分随
重合部分随![]() 的位置变化有三种情况:
的位置变化有三种情况:![]()
![]() 在
在![]() 之间;
之间;![]()
![]() 在
在![]() 上;
上;![]()
![]() 在
在![]() 之外.
之外.
![]()
![]() 在
在![]() 之
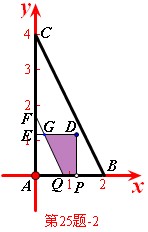
之![]() 间;如图(第25题-2),此时,正方形
间;如图(第25题-2),此时,正方形![]()
![]() 和梯形
和梯形![]() 重合部分为直角梯形,由(2)得:
重合部分为直角梯形,由(2)得:![]() 、
、![]() 、
、![]() 、过
、过![]() 的一次函数的解析式为:
的一次函数的解析式为:![]() 、设
、设![]() 与
与![]() 的交点为
的交点为![]() ,
,
解![]() ,得:
,得:![]() .
.
所以,![]() ,
,
![]() ,
,
此时:![]() .
.
![]()
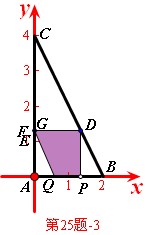
![]() 在
在![]() 上;如图(第25题-3),
上;如图(第25题-3),![]() 满足过
满足过![]() 的一次函数的解析式:
的一次函数的解析式:![]() ,
,
即:![]() ,
,![]() ,
,
把![]() 代入
代入![]() 的一次函数的解析式得:
的一次函数的解析式得:
![]() ,
,![]() ,
,
所以![]() 为同一点,所以:
为同一点,所以:![]() ,
,![]() ,此时:
,此时:![]()
![]()
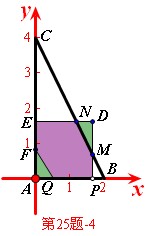
![]() 在
在![]() 之外.如图(第25题-4),设
之外.如图(第25题-4),设![]() 与
与![]() 相交于
相交于![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,
,
 解
解![]() 得:
得:![]() ;
;
解![]() 得:
得:![]() .
.
所以,![]()
![]()
此时:
![]()
![]()
综合![]() 、
、![]() 、
、![]() ,得点
,得点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点),正方形
两点),正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为:
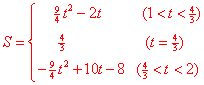

 智慧小复习系列答案
智慧小复习系列答案
 中,
中,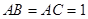 ,
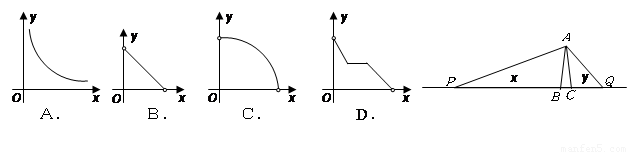
,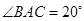 .动点P、Q分别在直线
.动点P、Q分别在直线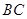 上运动,且始终保持
上运动,且始终保持 .设
.设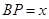 ,
,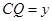 ,则
,则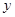 与
与 的函数关系的图象大致可以表示为
的函数关系的图象大致可以表示为 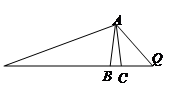
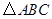 中,
中,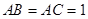 ,
,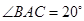 .动点P、Q分别在直线
.动点P、Q分别在直线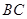 上运动,且始终保持
上运动,且始终保持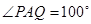 .设
.设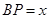 ,
,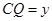 ,则
,则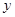 与
与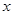 的函数关系的图象大致可以表示为
的函数关系的图象大致可以表示为 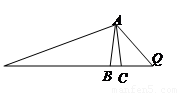
 中,
中,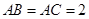 ,
, .动点
.动点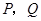 分别在直线
分别在直线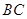 上运动,且始终保持
上运动,且始终保持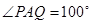 .设
.设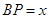 ,
,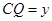 ,则
,则 与
与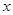 之间的函数关系用图象大致可以表示为( )
之间的函数关系用图象大致可以表示为( )