题目内容
1.边心距为$\sqrt{3}$的正六边形的面积为6$\sqrt{3}$.分析 根据题意画出图形,先求出∠AOB的度数,证明△AOB是等边三角形,得出AB=OA,再根据直角三角形的性质求出OA的长,再根据S六边形=6S△AOB即可得出结论.
解答 解:∵图中是正六边形,
∴∠AOB═60°.
∵OA=OB,
∴△OAB是等边三角形.
∴OA=OAB=AB,
∵OD⊥AB,OD=$\sqrt{3}$,
∴OA=$\frac{OD}{sin60°}$=2.
∴AB=4,
∴S△AOB=$\frac{1}{2}$AB×OD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∴正六边形的面积=6S△AOB=6×$\sqrt{3}$=6$\sqrt{3}$.
故答案为:6$\sqrt{3}$.
点评 本题考查的是正多边形和圆,熟知正六边形的性质,求出△AOB的面积是解答此题的关键.

练习册系列答案
相关题目
16. 有理数在数轴上的对应点的位置如图所示,则下列结论正确的是( )
有理数在数轴上的对应点的位置如图所示,则下列结论正确的是( )
 有理数在数轴上的对应点的位置如图所示,则下列结论正确的是( )
有理数在数轴上的对应点的位置如图所示,则下列结论正确的是( )| A. | ab>0 | B. | a-b>0 | C. | $\frac{a}{b}>0$ | D. | b-a>0 |
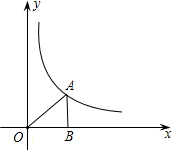 如图,A为反比例函数y=$\frac{k}{x}$的图象上一点,AB垂直x轴于B,若S△AOB=2,则k的值为( )
如图,A为反比例函数y=$\frac{k}{x}$的图象上一点,AB垂直x轴于B,若S△AOB=2,则k的值为( ) 如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC为$\frac{10\sqrt{3}}{3}$米.
如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC为$\frac{10\sqrt{3}}{3}$米.