题目内容
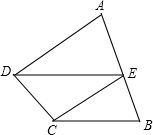如图，在四边形ABCD中，E是AB上一点，EC∥AD，DE∥BC，若S△BEC=1，S△ADE=3，则S△CDE等于
- A.
- B.
- C.
- D.2
C
分析：由题意在四边形ABCD中延长AD、BC交于F，则BECF为平行四边形，然后根据相似三角形面积之比等于边长比的平方来求解．
解答：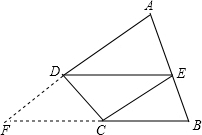
解：延长AD、BC交于F，则DECF为平行四边形，
∵EC∥AD，DE∥BC，
∴∠ADE=∠DEC=∠BCE，∠CBE=∠AED，
∴△CBE∽△DEA，
又∵S△BEC=1，S△ADE=3，
∴
=
=
，
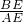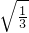∵CEDF为平行四边形，
∴△CDE≌△DCF，
∴S?CEDF=2S△CDE，
∵EC∥AD，
∴△BCE∽△BFA，
∴
=
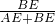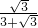，S△BCE：S△BFA=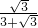（）2，即1：（1+3+2S△CDE）=
，
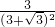解得：S△CDE=．
故选C．
点评：解答此题的关键是根据平行于三角形一边的直线截得的三角形与原三角形相似及相似三角形的性质来解答．
分析：由题意在四边形ABCD中延长AD、BC交于F，则BECF为平行四边形，然后根据相似三角形面积之比等于边长比的平方来求解．
解答：
解：延长AD、BC交于F，则DECF为平行四边形，∵EC∥AD，DE∥BC，
∴∠ADE=∠DEC=∠BCE，∠CBE=∠AED，
∴△CBE∽△DEA，
又∵S△BEC=1，S△ADE=3，
∴
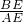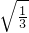==，∵CEDF为平行四边形，
∴△CDE≌△DCF，
∴S?CEDF=2S△CDE，
∵EC∥AD，
∴△BCE∽△BFA，
∴
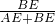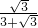=，S△BCE：S△BFA=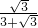（）2，即1：（1+3+2S△CDE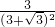）=，解得：S△CDE=
．故选C．
点评：解答此题的关键是根据平行于三角形一边的直线截得的三角形与原三角形相似及相似三角形的性质来解答．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
（2013•赤峰）如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．
已知：如图，在四边形ABC中，AD=BC，AB=CD．
如图，在Rt△ABC中，∠BAC=90°，将△ABC沿线段BC向右平移得到△DEF，使CE=AE，连结AD、AE、CD，则下列结论：①AD∥BE且AD=BE；②∠ABC=∠DEF；③ED⊥AC；④四边形AECD为菱形，其中正确的共有（ ）
已知：如图，在四边形ABC中，AD=BC，AB=CD．