��Ŀ����
����Ŀ����̽��֤������1��ij����ѧ����ѧϰС��Ծ������������ഹֱ���߶���������ڱߵ�������ϵ����̽��������������⣬�������֤����
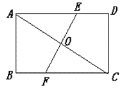
��ͼ�����ھ���ABCD�У�EF��GH��EF�ֱ�AD��BC�ڵ�E��F��GH�ֱ�AB��DC�ڵ�G��H����֤��![]() ��
��
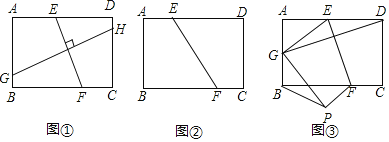
������Ӧ�ã���2����ͼ����������ABCD��EF�۵���ʹ�õ�B�͵�D�غϣ���AB��2��BC��3�����ۺ�EF�ij���
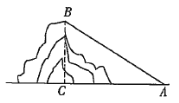
����չ���ã���3����ͼ����������ABCD��EF�۵���ʹ�õ�D����AB���ϵĵ�G������C���ڵ�P�����õ��ı���EFPG����AB��2��BC��3��EF��![]() ������BP�ij���
������BP�ij���
���𰸡���1������������2��EF��![]() ����3��BP��
����3��BP��![]() ��
��
��������
��1������A��AP��EF����BC��P������B��BQ��GH����CD��Q����ͼ1����֤AP=EF��GH=BQ����ABP�ס�BCQ��Ȼ���������������ε����ʾͿɽ�����⣻
(2)����BD�����ݾ��ε����ʵó�BD�ij����ٸ��ݽ��ۣ�1���ó�![]() �����������EF�ij�.
�����������EF�ij�.
��3������F��FH��EG��H������P��PJ��BF��J�����ݾ��ε����ʵõ�AD��CD�ij����ɽ��ۣ�1���ɵó�DG�ij������ɹ��ɶ����ó�AG�ij���Ȼ����ݷ��۵����ʽ�Ϲ��ɶ����ó��ı���HGPF�Ǿ��Σ������ó�FH�ij��ȣ����������������εó�BJ��PJ�ij��ȾͿ��Ե���BP�ij���.
��1����ͼ�٣�����A��AP��EF����BC��P������B��BQ��GH����CD��Q��BQ��AP��T��
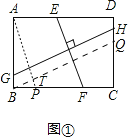
���ı���ABCD�Ǿ��Σ�
��AB��DC��AD��BC��
���ı���AEFP���ı���BGHQ����ƽ���ı��Σ�
��AP��EF��GH��BQ��
�֡�GH��EF��
��AP��BQ��
���BAT+��ABT��90����
���ı���ABCD�Ǿ��Σ�
���ABP����C��90����AD��BC��
���ABT+��CBQ��90����
���BAP����CBQ��
���ABP�ס�BCQ��
��![]() ,
,
��![]() .
.
��2����ͼ���У�����BD��
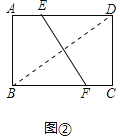
���ı���ABCD�Ǿ��Σ�
���C��90����AB��CD��2��
��BD��![]() ,
,
��D��B����EF�Գƣ�
��BD��EF��
��![]() ,
,
��![]() ,
,
��EF��![]() .
.
��3����ͼ���У�����F��FH��EG��H������P��PJ��BF��J��
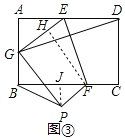
���ı���ABCD�Ǿ��Σ�
��AB��CD��2��AD��BC��3����A��90����
��![]() =
= ![]() ,
,
��DG��![]() ��
��
��AG��![]() ��1��
��1��
�ɷ��ۿ�֪��ED��EG����ED��EG��x��
��Rt��AEG����EG2��AE2+AG2��
��x2��AG2+AE2��
��x2����3��x��2+1��
��x��![]() ��
��
��DE��EG��![]() ��
��
��FH��EG��
���FHG����HGP����GPF��90����
���ı���HGPF�Ǿ��Σ�
��FH��PG��CD��2��
��EH��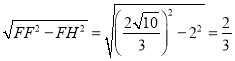 ��
��
��GH��FP��CF��EG��EH��![]() ��
��![]() ��1��
��1��
��PF��EG��EA��FB��
���AEG����JPF��
�ߡ�A����FJP��90����
���AEG�ס�JFP��
��![]() ��
��
��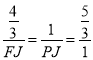 ��
��
��FJ��![]() ��PJ��
��PJ��![]() ��
��
��BJ��BC��FJ��CF��3��![]() ��1��
��1��![]() ��
��
��Rt��BJP��BP��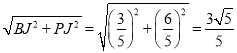 ��
��

 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�