Question

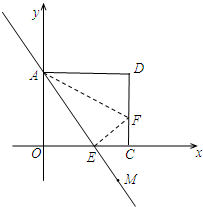如图，把矩形纸片AOCD置于直角坐标系中，O为坐标原点，AO=

3

，把矩形纸片沿直线AF折叠，使得点D与OC上的点E重合，这时AE平分∠OAF．
（1）填空：∠DAF

 

∠EAF（填“＞”、“＜”或“=”）；
（2）求出直线AE的解析式及点F的坐标；
（3）设点M是直线AE上的一个动点，过点M作AD的平行线，交y轴于点N，是否存在点M，使得以M、N、D、A为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．

Answer 1

分析：（1）根据折叠的性质直接得到∴∠DAF=∠EAF；
（2）由AE平分∠OAF，得到∠OAE=∠EAF，而∠DAF=∠EAF，则∠DAF=∠EAF=∠OAE=30°，根据含30°的直角三角形三边的关系得到OE=1，即A（0，

3

）、E（1，0），再利用待定系数法即可求出直线AE的解析式；设点F的坐标（x，y），利用折叠的性质和含30°的直角三角形三边的关系可得到CF=

3

3

，EC=1，即可得到F点的坐标．
（3）作DN∥AM交y轴于点N，过点N作MN⊥y轴交直线AE于点M，则四边形MADN是平行四边形，利用平行四边形的性质得到MN=AD=2，根据含30°的直角三角形三边的关系
得AN=

3

AD=2

3

，即可得到M点的坐标；同理可得当延长DC交直线AE于点M'，则DM'∥AO，作M'N'⊥y轴于点N'，则M'N'∥AD，求出点M′的坐标．

解答：解：（1）∵矩形纸片沿直线AF折叠，使得点D与OC上的点E重合，
∴∠DAF=∠EAF．
故答案为=；

（2）∵AE平分∠OAF，
∴∠OAE=∠EAF，
而∠DAF=∠EAF，
∴∠DAF=∠EAF=∠OAE=30°，
在Rt△OAE中，OA=

3

，
∴OE=OA•tan30°=1，
∴A（0，

3

）、E（1，0），
设直线AE的解析式为y=kx+b（k≠0），
∴

b= 3 k+b=0

，解得：

k=- 3 b= 3

∴直线AE的解析式为y=-

3

x+

3

；
∵∠AEO=60°，∠AEF=90°，
∴∠FEC=30°
设点F的坐标（x，y），则CF=y，
∴EF=DF=2y
又DF=DC-DF，
∴DF=

3

-y，
∴2y=

3

-y，解得y=

3

3

，
又EC=

3

CF=1，
∴OC=2，
∴F（2，

3

3

）；

（3）存在．理由如下：
如图，作DN∥AM交y轴于点N，过点N作MN⊥y轴交直线AE于点M，
则MN∥AD，
∴四边形MADN是平行四边形．
∴MN=AD=2，
又∠OAE=∠MAN=30°．
∴AN=

3

AD=2

3

，
∴点M(-2，3

3

)；
延长DC交直线AE于点M'，则DM'∥AO，
作M'N'⊥y轴于点N'，则M'N'∥AD，
∴四边形AN'M'D是平行四边形．
∴N'M'=OC=2
又点M'在直线y=-

3

x+

3

上，当x=2时，y=-2

3

+

3

=-

3

，
∴点M′(2，-

3

)
综上，存在2个符合条件的点M坐标，它们是(-2，3

3

)或(2，-

3

)．

点评：本题考查了利用待定系数法求直线解析式的方法；也考查了折叠的性质、含30°的直角三角形三边的关系以及平行四边形的性质．