题目内容
已知二次函数y=x2+（2m+1）x+m2-1的最小值是-2，则m= ．
【答案】分析：对二次函数y=x2+（2m+1）x+m2-1，a＞0，则在顶点处取得最小值，顶点纵坐标y=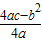
=-2，代入求得m的值．
解答：解：在二次函数y=x2+（2m+1）x+m2-1中，a=1＞0，则有最小值，且在顶点取得，
又顶点纵坐标y=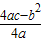
=
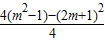=-2，
解得：m=
．
点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法．
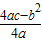=-2，代入求得m的值．解答：解：在二次函数y=x2+（2m+1）x+m2-1中，a=1＞0，则有最小值，且在顶点取得，
又顶点纵坐标y=
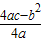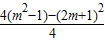==-2，解得：m=
．点评：求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．