题目内容
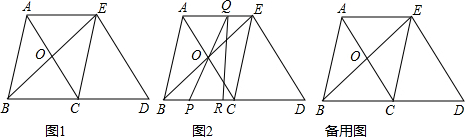
10. 如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).(1)用含t的代数式表示:
AP=t;DP=12-t;BQ=15-2t;CQ=2t.
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
分析 (1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
解答 解:(1)t,12-t,15-2t,2t
(2)根据题意有AP=t,CQ=2t,PD=12-t,BQ=15-2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,解得t=5.
∴t=5s时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD-AP=12-t,
如图1,∵AD∥BC,∴当PD=QC时,四边形PDCQ是平行四边形.
即:12-t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
点评 本题考查了平行四边形的判定和性质的应用,题目是一道综合性比较强的题目,难度适中,解题的关键是把握“化动为静”的解题思想.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
20.下列从左到右的变形中,是因式分解的是( )
| A. | x2-6x+9=x(x-6-9) | B. | (a+2)(a-2)=a2-4 | C. | 2a(b-c)=2ab-2bc | D. | y2-4y+4=(y-2)2 |
1.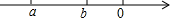 已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
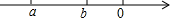 已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )| A. | a-1>b-1 | B. | 3a>3b | C. | -a>-b | D. | a+b>a-b |
2.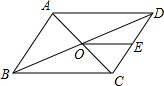 如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
 如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )
如图,?ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是( )| A. | 24 | B. | 15 | C. | 21 | D. | 30 |
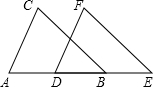 把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.
把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:(1)∠C=∠F;(2)AC∥DF.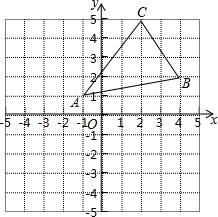 如图,将三角形ABC向左平移3个单位长度,在向下平移4个单位长度,得到三角形A1B1C1.
如图,将三角形ABC向左平移3个单位长度,在向下平移4个单位长度,得到三角形A1B1C1.