题目内容

已知开口向下的抛物线y=mx²-2x+m²-4经过原点，则m的值为

-2

-2

．

分析：先把原点坐标代入二次函数的解析式中可求出m=2或m=-2，由于抛物线开口向下，根据二次函数的性质得到m＜0，则m=-2．

解答：解：把（0，0）代入y=mx²-2x+m²-4得m²-4=0，解得m=2或m=-2，
∵抛物线开口向下，
∴m＜0，
∴m=-2．
故答案为-2．

点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上的点满足y=ax²+bx+c（a、b、c为常数，a≠0）．也考查了二次函数的性质．

练习册系列答案

最新中考信息卷系列答案

红对勾中考分类训练系列答案

红色风暴初中生学业考试模拟与预测系列答案

鸿图图书寒假作业假期作业吉林大学出版社系列答案

中考新概念系列答案

互联网多功能作业本系列答案

黄冈金牌之路妙解教材系列答案

黄冈金牌之路中考精英总复习系列答案

中考新夺标试题研究系列答案

汇测初中英语系列答案

相关题目

已知开口向下的抛物线y=ax²+bx+c与x轴交于M，N两点（点N在点M的右侧），并且M和N两点的横坐标分别是方程x²-2x-3=0的两根，点K是抛物线与y轴的交点，∠MKN不小于90度．
（1）求点M和N的坐标；
（2）求系数a的取值范围；
（3）当y取得最大值时，抛物线上是否存在点P，使得S△MPN=2

？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．

已知开口向下的抛物线y=ax²+bx+c与x轴交于M，N两点（点N在点M的右侧），并且M和N两点的横坐标分别是方程x²-2x-3=0的两根，点K是抛物线与y轴的交点，∠MKN不小于90度．
（1）求点M和N的坐标；
（2）求系数a的取值范围；
（3）当y取得最大值时，抛物线上是否存在点P，使得 $数学公式$ ？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．

（2000•甘肃）已知开口向下的抛物线y=ax²+bx+c与x轴交于M，N两点（点N在点M的右侧），并且M和N两点的横坐标分别是方程x²-2x-3=0的两根，点K是抛物线与y轴的交点，∠MKN不小于90度．
（1）求点M和N的坐标；
（2）求系数a的取值范围；
（3）当y取得最大值时，抛物线上是否存在点P，使得

？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．

（2000•甘肃）已知开口向下的抛物线y=ax²+bx+c与x轴交于M，N两点（点N在点M的右侧），并且M和N两点的横坐标分别是方程x²-2x-3=0的两根，点K是抛物线与y轴的交点，∠MKN不小于90度．
（1）求点M和N的坐标；
（2）求系数a的取值范围；
（3）当y取得最大值时，抛物线上是否存在点P，使得

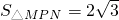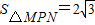？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．