题目内容
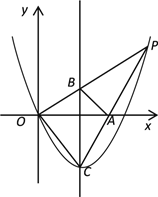
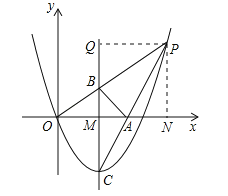
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
【答案】(1) y=x2-2x;(2)BC=m-1;(3) P的坐标为(![]() )
)
【解析】分析:(1)由对称轴公式,以及已知顶点C坐标,利用待定系数法确定出解析式即可;
(2)设出P坐标,令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N,表示出PN,ON,OM,利用比例表示出BM,进而表示出BC即可;
(3)设出P坐标,由两三角形面积相等得到AC=AP,过点P作PQ⊥BC交BC于点Q,列出关于t的方程,求出方程的解确定出t的值,即可求出P坐标.
详解:(1)∵抛物线y=ax2+bx的顶点为C(1,﹣1),∴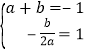 ,解得:
,解得:![]() ,∴抛物线的表达式为:y=x2﹣2x;
,∴抛物线的表达式为:y=x2﹣2x;
(2)∵点P的横坐标为m,∴点P的纵坐标为:m2﹣2m,令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N.∵P是抛物线上位于第一象限内的一点,∴PN=m2﹣2m,ON=m,OM=1,由![]() =
=![]() ,得:
,得:![]() =
=![]() ,∴BM=m﹣2.∵点C的坐标为(1,﹣1),∴BC=m﹣2+1=m﹣1;
,∴BM=m﹣2.∵点C的坐标为(1,﹣1),∴BC=m﹣2+1=m﹣1;
(3)令P(t,t2﹣2t).∵△ABP的面积等于△ABC的面积,∴AC=AP,过点P作PQ⊥BC交BC于点Q,∴CM=MQ=1,可得:t2﹣2t=1,解得:t=1+![]() (t=1﹣
(t=1﹣![]() 舍去),∴P的坐标为(1+
舍去),∴P的坐标为(1+![]() ,1).
,1).

练习册系列答案
相关题目