Question

（1）求不等式组的整数解．
（2）先化简，再求值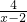：（-）÷，其中x是方程x²=2x的根．

Answer 1

解：（1），
①式解得：x＜2
②式解得：x≥-1，
则-1≤x＜2，
故不等式组的整数解为：-1、0、1；

（2）原式=.
=
∵x²=2x，
∴x₁=0，x₂=2
∵x≠2，
∴当x=0时原式=-1．
分析：（1）分别求出各不等式的解集，再求出其公共解集即可；
（2）先根据分式混合运算的法则把原式进行化简，再根据x是方程x²=2x的根求出x的值，代入原式进行计算即可．
点评：本题考查的是分式的化简求值，在解答（2）时要保证分式有意义．