题目内容
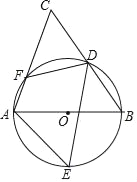
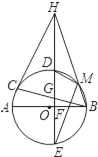
【题目】如图,AB,BC分别是⊙O的直径和弦,点D为![]() 上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
求证:
(1)DE⊥AB;
(2)∠HMD=∠MHE+∠MEH.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)连接OC,根据等边对等角和切线的性质,证明∠BFG=∠OCH=90°即可;
(2)连接BE,根据垂径定理和圆内接四边形的性质,得出∠HMD=∠BME,再根据三角形的外角的性质证明∠HMD=∠DEB=∠EMB即可.
详解:证明:(1)连接OC,
∵HC=HG,
∴∠HCG=∠HGC;
∵HC切⊙O于C点,
∴∠OCB+∠HCG=90°;
∵OB=OC,
∴∠OCB=∠OBC,
∵∠HGC=∠BGF,
∴∠OBC+∠BGF=90°,
∴∠BFG=90°,即DE⊥AB;
(2)连接BE,
由(1)知DE⊥AB,
∵AB是⊙O的直径,
∴![]() ,
,
∴∠BED=∠BME;
∵四边形BMDE内接于⊙O,
∴∠HMD=∠BED,
∴∠HMD=∠BME;
∵∠BME是△HEM的外角,
∴∠BME=∠MHE+∠MEH,
∴∠HMD=∠MHE+∠MEH.


 名校课堂系列答案
名校课堂系列答案【题目】在汛期来临之前,某市提前做好防汛工作,该市的![]() 、
、![]() 两乡镇急需防汛物质分别为80吨和120吨,由该市的甲、乙两个地方负责全部运送到位,甲、乙两地有防汛物质分别为110吨和90吨,已知甲、乙两地运到
两乡镇急需防汛物质分别为80吨和120吨,由该市的甲、乙两个地方负责全部运送到位,甲、乙两地有防汛物质分别为110吨和90吨,已知甲、乙两地运到![]() 、
、![]() 两乡镇的每吨物质的运费如表所示:
两乡镇的每吨物质的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设乙地运到![]() 乡镇的防汛物质为
乡镇的防汛物质为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并指出
(吨)的函数关系式,并指出![]() 的取值范围.
的取值范围.
(2)求最低总运费,并说明总运费最低时的运送方案.
【题目】学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,下表记录了A、B、C三名学生的得分情况,则参赛学生D的得分可能是( )
参赛学生 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 14 | 6 | 64 |
A.66B.93C.40D.87