Question

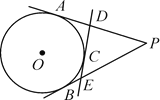
【题目】如图，在平面直角坐标系中，以坐标原点O为圆心，2为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与轴相交于点A，与轴相交于点B。

（1）点P在运动时，线段AB的长度页在发生变化，请写出线段AB长度的最小值，并说明理由；

（2）在⊙O上是否存在一点Q，使得以Q、O、A、P为顶点的四边形时平行四边形？若存在，请求出Q点的坐标；若不存在，请说明理由。

Answer 1

【答案】（1）线段AB长度的最小值为4

理由如下：

连接OP因为AB切⊙O于P，所以OP⊥AB

取AB的中点C，则…………3分

当时，OC最短，

即AB最短，此时…………4分

（2）设存在符合条件的点Q，

如图①，

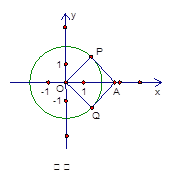
设四边形APOQ为平行四边形，

因为四边形APOQ为矩形

又因为

所以四边形APOQ为正方形

所以，

在Rt△OQA中，根据，

得Q点坐标为（）。 …………7分

如图②，设四边形APQO为平行四边形

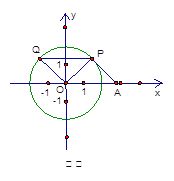
因为OQ∥PA，，

所以，

又因为

所以，

因为 PQ∥OA，

所以轴。

设轴于点H，

在Rt△OHQ中，根据，

得Q点坐标为（）

所以符合条件的点Q的坐标为（）或（）。

【解析】

（1）如图，设AB的中点为C，连接OP，由于AB是圆的切线，故△OPC是直角三角形，有OP＜OC，所以当OC与OP重合时，OC最短；

（2）分两种情况：如图（1），当四边形APOQ是正方形时，△OPA，△OAQ都是等腰直角三角形，可求得点Q的坐标为（，﹣），如图（2），可求得∠QOP=∠OPA=90°，由于OP=OQ，故△OPQ是等腰直角三角形，可求得点Q的坐标为（﹣，）．