题目内容
 已知:如图,在△ABC中,AB=AC=2,∠B=15°.过点C作CD⊥BA,交BA的延长线于点D,求△ACD的周长.
已知:如图,在△ABC中,AB=AC=2,∠B=15°.过点C作CD⊥BA,交BA的延长线于点D,求△ACD的周长.
解: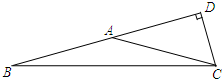 如图,在△ABC中,AB=AC=2,∠B=15°,
如图,在△ABC中,AB=AC=2,∠B=15°,
∴∠B=∠ACB=15°,
∴∠DAC=2∠B=30°.
又∵CD⊥BA,
∴CD= AC=1,
AC=1,
∴根据勾股定理得到AD= =
= ,
,
∴△ACD的周长=AD+CD+AC= +1+2=
+1+2= +3.
+3.
答:△ACD的周长是 +3.
+3.
分析:利用等腰三角形的性质、三角形外角定理即可求得Rt△ADC的内角∠DAC=30°,则CD= AC=1,由勾股定理求得AD=
AC=1,由勾股定理求得AD= ,然后根据三角形的周长公式进行解答.
,然后根据三角形的周长公式进行解答.
点评:本题综合考查了勾股定理、含30度角的直角三角形、等腰三角形的性质.注意,勾股定理适用于直角三角形中.
 如图,在△ABC中,AB=AC=2,∠B=15°,
如图,在△ABC中,AB=AC=2,∠B=15°,∴∠B=∠ACB=15°,
∴∠DAC=2∠B=30°.
又∵CD⊥BA,
∴CD=
 AC=1,
AC=1,∴根据勾股定理得到AD=
 =
= ,
,∴△ACD的周长=AD+CD+AC=
 +1+2=
+1+2= +3.
+3.答:△ACD的周长是
 +3.
+3.分析:利用等腰三角形的性质、三角形外角定理即可求得Rt△ADC的内角∠DAC=30°,则CD=
 AC=1,由勾股定理求得AD=
AC=1,由勾股定理求得AD= ,然后根据三角形的周长公式进行解答.
,然后根据三角形的周长公式进行解答.点评:本题综合考查了勾股定理、含30度角的直角三角形、等腰三角形的性质.注意,勾股定理适用于直角三角形中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,