��Ŀ����
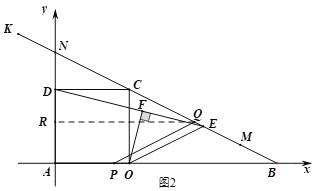
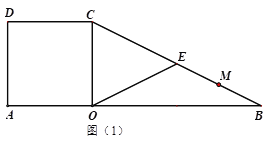
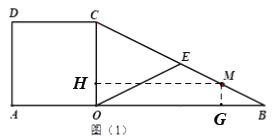
����Ŀ����ͼ��1�����ڱ߳�Ϊ4��������![]() �У���AO���ӳ�����ȡ��B��ʹOB=2OA������BC��
�У���AO���ӳ�����ȡ��B��ʹOB=2OA������BC��
��1����![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() �����߶�
�����߶�![]() �ij���
�ij���
��2����M���߶�BC�ϣ��ҵ�OB��OC�ľ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ʱ�� ��
ʱ�� ��![]() ��
��![]() ��ֵ��
��ֵ��
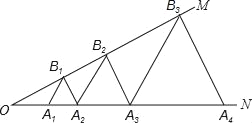
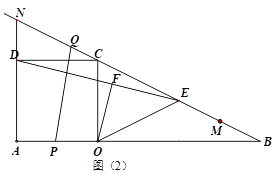
��3����ͼ��2�����ڵڣ�1������2���������£��ӳ�![]() ��ֱ��
��ֱ��![]() �ڵ�N������
�ڵ�N������![]() ��
��![]() �ϴӵ�
�ϴӵ�![]() ���յ�
���յ�![]() �����˶���ͬʱ������
�����˶���ͬʱ������![]() ��
��![]() �ӳ����ϣ���ֱ��
�ӳ����ϣ���ֱ��![]() ���յ�M�����˶�������ͬʱ������ͬʱ�����յ㣮����
���յ�M�����˶�������ͬʱ������ͬʱ�����յ㣮����![]() �˶���
�˶���![]() �е�ʱ����
�е�ʱ����![]() ǡ�����
ǡ�����![]() �غϣ�
�غϣ�
�����˶������У����![]() ���˶�·��Ϊs��
���˶�·��Ϊs��![]() ���ú�t�Ĵ���ʽ��ʾs��
���ú�t�Ĵ���ʽ��ʾs��
�ڹ���O��![]() �ڵ�
�ڵ�![]() �����˶�·���У���
�����˶�·���У���![]() ��
��![]() ��һ��ƽ��ʱ������������������
��һ��ƽ��ʱ������������������![]() �ij���
�ij���
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3����
����3����![]() ����
����![]() ��
��![]() .
.
��������
��1���ȸ��ݹ��ɶ������BC�ij���������ֱ�������ε����ʼ�����ý����
��2������M��MG��OB��MH��OC������֤��BMG�ס�BCO���������������ε����ʲ������֪![]() �������m��n��ֵ��
�������m��n��ֵ��
��3����������֪������![]() �˶���
�˶���![]() �е�ʱ����
�е�ʱ����![]() ǡ�����
ǡ�����![]() �غϣ����Ե���
�غϣ����Ե���![]() ��
��![]() �е��˶�����Oʱ����
�е��˶�����Oʱ����![]() ǡ����ӵ�
ǡ����ӵ�![]() �˶�����M���ݴ��г�����ʽ���ɵó�s��t�Ĺ�ϵʽ��
�˶�����M���ݴ��г�����ʽ���ɵó�s��t�Ĺ�ϵʽ��
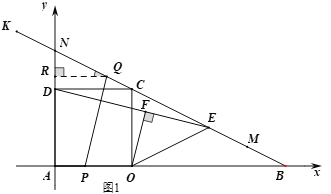
����ȷ����Q�ij�����K��λ�ã����������![]() ���ٽ�����ͼ1��ʾ��ƽ��ֱ������ϵ����Ȼ�ڵ�P���˶������У�PQ��DEʼ�ղ�ƽ�У���PQ��OFʱ����������ϵ������ֱ�ߴ�ֱʱ����
���ٽ�����ͼ1��ʾ��ƽ��ֱ������ϵ����Ȼ�ڵ�P���˶������У�PQ��DEʼ�ղ�ƽ�У���PQ��OFʱ����������ϵ������ֱ�ߴ�ֱʱ����![]() ��������ú�t�IJ�����ʾ��ֱ��PQ�Ľ���ʽ������ֱ��BC�����������������Q�����꣬Ȼ������������Ǻ�����֪ʶ���QNֵ������QK�ij��������âٵĽ��ۼ��ù���t�ķ��̣��ⷽ�̼������t��ֵ����PQ��OEʱ����ͼ2����������ϵ����ֱ��ƽ��
��������ú�t�IJ�����ʾ��ֱ��PQ�Ľ���ʽ������ֱ��BC�����������������Q�����꣬Ȼ������������Ǻ�����֪ʶ���QNֵ������QK�ij��������âٵĽ��ۼ��ù���t�ķ��̣��ⷽ�̼������t��ֵ����PQ��OEʱ����ͼ2����������ϵ����ֱ��ƽ��![]() ��ͬ�����˼·��⼴��.
��ͬ�����˼·��⼴��.
�⣺��1�����ı���![]() �������Σ���OC=AO=4����COA=90�������COB=90����
����������OC=AO=4����COA=90�������COB=90����
��OB=2OA����OB=8����![]() ��
��
�ߵ�![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() ��
��
��2����ͼ��1��������M��MG��OB��MH��OC����MG=m��MH=n=OG��MG��OC��
���BMG�ס�BCO����![]() ����
����![]() ��
��
��![]() ����n=6mʱ��
����n=6mʱ��![]() ����ã�m=1����n=6��
����ã�m=1����n=6��
��![]() ��
��![]() ��
��
��3����������֪������![]() �˶���
�˶���![]() �е�ʱ����
�е�ʱ����![]() ǡ�����
ǡ�����![]() �غϣ����Ե���
�غϣ����Ե���![]() ��
��![]() �е��˶�����Oʱ����
�е��˶�����Oʱ����![]() ǡ����ӵ�
ǡ����ӵ�![]() �˶�����M.
�˶�����M.
��ͼ��1������CH=3��HM=6����![]() ��
��
������![]() ����
����![]() ��
��
����BC�ӳ�����ȡ��K��ʹCK=CM=![]() ����
����![]() ����
����![]() ���������֪����Q�ij�������ǵ�K.
���������֪����Q�ij�������ǵ�K.
������ͼ1��ʾ��ƽ��ֱ������ϵ��
��PQ��OFʱ��PQ��DE��
��D��0��4����E��8��2������ֱ��DE�Ľ���ʽΪ��![]() ��������
��������![]() ������P��t��0������ã�
������P��t��0������ã�![]() ����
����![]() ��
��
��C��4��4����B��12��0������ֱ��BD�Ľ���ʽΪ��![]() ��
��
���������飺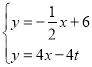 �����
�����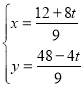 ��
��
���Q��![]() ��
��![]() ����
����
����Q��QR��y���ڵ�R����![]() ��
��
��ֱ����QRN�У�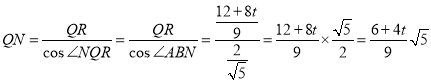 ��
��
��![]() ��
��
�ɢ�֪��![]() ����
����![]() =
=![]() ����ã�
����ã�![]() ��
��
��PQ��OEʱ����ͼ2��
��O��4��0����E��8��2������ֱ��OE�Ľ���ʽΪ��![]() ��
��
����ֱ��PQ�Ľ���ʽΪ��![]() ����P��t��0������ã�
����P��t��0������ã�![]() ��
��
��![]() ��
��
���������飺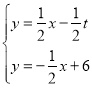 ����ã�
����ã�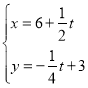 ����Q��
����Q��![]() ��
��![]() ����
����
����Q��QR��y���ڵ�R����![]() ��
��
��ֱ�ǡ�QRN�У�![]() ��
��
��![]() ��
��
�ɢ�֪��![]() ����
����![]() =
=![]() ����ã�
����ã�![]() ��
��
��Ȼ�ڵ�P���˶������У�PQ��DEʼ�ղ�ƽ�У�
���ϣ���![]() ��
��![]() ��һ��ƽ��ʱ��
��һ��ƽ��ʱ��![]() ��
��![]() .
.