题目内容
若实数x≠y,且满足(x+1)2+2(x+1)-2=0,y2+4y+1=0.则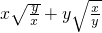 =
=
- A.2
- B.4
- C.±2
- D.-2
D
分析:先化简(x+1)2+2(x+1)-2=0,可得x2+4x+1=0,根据题意可知x、y是方程a2+4a+1=0的两根,再化简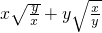 ,根据根与系数的关系即可求解.
,根据根与系数的关系即可求解.
解答:化简(x+1)2+2(x+1)-2=0,可得x2+4x+1=0,
∵x≠y,y2+4y+1=0.
∴x<0,y<0,xy=1,
∴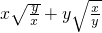 =-
=- -
- =-2
=-2 =-2.
=-2.
故选D.
点评:考查了二次根式的化简求值,一元二次方程根与系数的关系,二次根式的性质: =|a|的知识点.
=|a|的知识点.
分析:先化简(x+1)2+2(x+1)-2=0,可得x2+4x+1=0,根据题意可知x、y是方程a2+4a+1=0的两根,再化简
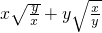 ,根据根与系数的关系即可求解.
,根据根与系数的关系即可求解.解答:化简(x+1)2+2(x+1)-2=0,可得x2+4x+1=0,
∵x≠y,y2+4y+1=0.
∴x<0,y<0,xy=1,
∴
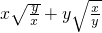 =-
=- -
- =-2
=-2 =-2.
=-2.故选D.
点评:考查了二次根式的化简求值,一元二次方程根与系数的关系,二次根式的性质:
 =|a|的知识点.
=|a|的知识点. 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.