题目内容
(2013•惠山区一模)已知二次函数y=ax2+bx+3的图象经过(1,
),(2,
)两点,与x轴的两个交点的右边一个交点为点A,与y轴交于点B.
(1)求此二次函数的解析式并画出这个二次函数的图象;
(2)求线段AB的中垂线的函数解析式.
| 21 |
| 4 |
| 11 |
| 2 |
(1)求此二次函数的解析式并画出这个二次函数的图象;
(2)求线段AB的中垂线的函数解析式.
分析:(1)将(1,
),(2,
)代入y=ax2+bx+3,利用待定系数法求得二次函数的解析式,再根据二次函数的性质即可画出这个二次函数的图象;
(2)根据二次函数的解析式为y=-x2+
x+3,求出A、B两点的坐标.连接AB,作线段AB的中垂线MN,交AB于M,交OA于N,则点M为AB的中点,根据中点坐标公式得到M点坐标为(2,
).设N点坐标为(x,0),则ON=x,根据线段垂直平分线的性质得出AN=BN=4-x,然后在直角△OBN中,由勾股定理得出OB2+ON2=BN2,求出x的值,得到N点坐标为(
,0).设直线MN的解析式为y=mx+n,将M,N两点的坐标代入,运用待定系数法即可求解.
| 21 |
| 4 |
| 11 |
| 2 |
(2)根据二次函数的解析式为y=-x2+
| 13 |
| 4 |
| 3 |
| 2 |
| 7 |
| 8 |
解答: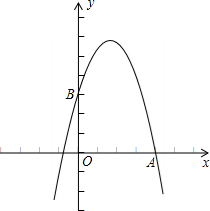 解:(1)∵二次函数y=ax2+bx+3的图象经过(1,
解:(1)∵二次函数y=ax2+bx+3的图象经过(1,
),(2,
)两点,
∴将两点坐标代入二次函数解析式,
得:
,
解得:
,
∴此二次函数的解析式为y=-x2+
x+3.
图象如右所示:
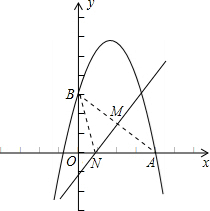 (2)解方程-x2+
(2)解方程-x2+
x+3=0,
即4x2-13x-12=0,
解得x1=4,x2=-
.
∵抛物线y=-x2+
x+3与x轴的两个交点的右边一个交点为点A,与y轴交于点B,
∴A点坐标为(4,0),B点坐标为(0,3).
连接AB,作线段AB的中垂线MN,交AB于M,交OA于N,连接BN,则点M为AB的中点,其坐标为(2,
).
设N点坐标为(x,0),则ON=x,AN=BN=4-x,
在△OBN中,∵∠BON=90°,OB=3,ON=x,BN=4-x,
∴OB2+ON2=BN2,即32+x2=(4-x)2,
解得x=
,
∴N点坐标为(
,0).
设直线MN的解析式为y=mx+n,
将M(2,
),N(
,0)代入,
得
,
解得
,
∴直线MN的解析式为y=
x-
.
即线段AB的中垂线的函数解析式为y=
x-
.
 解:(1)∵二次函数y=ax2+bx+3的图象经过(1,
解:(1)∵二次函数y=ax2+bx+3的图象经过(1,| 21 |
| 4 |
| 11 |
| 2 |
∴将两点坐标代入二次函数解析式,
得:
|
解得:
|
∴此二次函数的解析式为y=-x2+
| 13 |
| 4 |
图象如右所示:
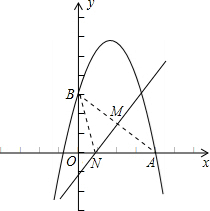 (2)解方程-x2+
(2)解方程-x2+| 13 |
| 4 |
即4x2-13x-12=0,
解得x1=4,x2=-
| 3 |
| 4 |
∵抛物线y=-x2+
| 13 |
| 4 |
∴A点坐标为(4,0),B点坐标为(0,3).
连接AB,作线段AB的中垂线MN,交AB于M,交OA于N,连接BN,则点M为AB的中点,其坐标为(2,
| 3 |
| 2 |
设N点坐标为(x,0),则ON=x,AN=BN=4-x,
在△OBN中,∵∠BON=90°,OB=3,ON=x,BN=4-x,
∴OB2+ON2=BN2,即32+x2=(4-x)2,
解得x=
| 7 |
| 8 |
∴N点坐标为(
| 7 |
| 8 |
设直线MN的解析式为y=mx+n,
将M(2,
| 3 |
| 2 |
| 7 |
| 8 |
得
|
解得
|
∴直线MN的解析式为y=
| 4 |
| 3 |
| 7 |
| 6 |
即线段AB的中垂线的函数解析式为y=
| 4 |
| 3 |
| 7 |
| 6 |
点评:本题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解析式,二次函数的图象与性质,二次函数图象上点的坐标特征,勾股定理,中点坐标公式,线段垂直平分线的性质,综合性较强,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
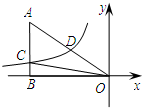 (2013•惠山区一模)如图,已知双曲线
(2013•惠山区一模)如图,已知双曲线