题目内容
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.

(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
【答案】
解:(1)AF与圆O的相切。理由为:
如图,连接OC,

∵PC为圆O切线,∴CP⊥OC。
∴∠OCP=90°。
∵OF∥BC,
∴∠AOF=∠B,∠COF=∠OCB。
∵OC=OB,∴∠OCB=∠B。∴∠AOF=∠COF。
∵在△AOF和△COF中,OA=OC,∠AOF=∠COF,OF=OF,
∴△AOF≌△COF(SAS)。∴∠OAF=∠OCF=90°。
∴AF为圆O的切线,即AF与⊙O的位置关系是相切。
(2)∵△AOF≌△COF,∴∠AOF=∠COF。
∵OA=OC,∴E为AC中点,即AE=CE= AC,OE⊥AC。
AC,OE⊥AC。
∵OA⊥AF,∴在Rt△AOF中,OA=4,AF=3,根据勾股定理得:OF=5。
∵S△AOF= •OA•AF=
•OA•AF= •OF•AE,∴AE=
•OF•AE,∴AE= 。
。
∴AC=2AE= 。
。
【解析】
试题分析:(1)AF与圆O的相切,理由为:连接OC,由PC为圆O的切线,利用切线的性质得到CP垂直于OC,由OF与BC平行,利用两直线平行内错角相等,同位角相等,分别得到两对角相等,根据OB=OC,利用等边对等角得到一对角相等,等量代换得到一对角相等,再由OC=OA,OF为公共边,利用SAS得出△AOF与△COF全等,由全等三角形的对应角相等及垂直定义得到AF垂直于OA,即可得证。
(2)由AF垂直于OA,在RtAOF中,由OA与AF的长,利用勾股定理求出OF的长,而OA=OC,OF为角平分线,利用三线合一得到E为AC中点,OE垂直于AC,利用面积法求出AE的长,即可确定出AC的长。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
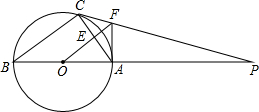 (2013•铁岭)如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(2013•铁岭)如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.