Question

已知：如图，D是△ABC内的任意一点．求证：∠BDC=∠1+∠A+∠2．

Answer 1

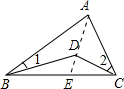证明：连接AD并延长交BC于点E，
∵∠BDE是△ABD的外角，
∴∠BDE=∠1+∠BAD，∠CDE=∠CAD+∠2，
∴∠BDE+∠CDE=∠1+∠BAD+∠CAD+∠2，
∵∠BAD+∠CAD=∠A，∠BDC=∠BDE+∠CDE，
∴∠BDC=∠1+∠A+∠2．
分析：连接AD并延长交BC于点E，再根据三角形内角与外角的关系即可解答．
点评：此题比较简单，考查的是三角形内角与外角的关系，解答此题的关键是作出辅助线，构造出三角形，再利用三角形内角与外角的关系求解．