题目内容
 (2013•遵义)如图,已知直线y=
(2013•遵义)如图,已知直线y=| 1 |
| 2 |
| k |
| x |
| k |
| x |
(2,4)或(8,1)
(2,4)或(8,1)
.分析:把点B的坐标代入反比例函数解析式求出k值,再根据反比例函数图象的中心对称性求出点A的坐标,然后过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,
),然后根据S△AOC=S△COF+S梯形ACFE-S△AOE列出方程求解即可得到a的值,从而得解.
| 8 |
| a |
解答: 解:∵点B(-4,-2)在双曲线y=
解:∵点B(-4,-2)在双曲线y=
上,
∴
=-2,
∴k=8,
根据中心对称性,点A、B关于原点对称,
所以,A(4,2),
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,
),
若S△AOC=S△COF+S梯形ACFE-S△AOE,
=
×8+
×(2+
)(4-a)-
×8,
=4+
-4,
=
,
∵△AOC的面积为6,
∴
=6,
 整理得,a2+6a-16=0,
整理得,a2+6a-16=0,
解得a1=2,a2=-8(舍去),
∴
=
=4,
∴点C的坐标为(2,4).
若S△AOC=S△AOE+S梯形ACFE-S△COF=
,
∴
=6,
解得:a=8或a=-2(舍去)
∴点C的坐标为(8,1).
故答案为:(2,4)或(8,1).
 解:∵点B(-4,-2)在双曲线y=
解:∵点B(-4,-2)在双曲线y=| k |
| x |
∴
| k |
| -4 |
∴k=8,
根据中心对称性,点A、B关于原点对称,
所以,A(4,2),
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为(a,
| 8 |
| a |
若S△AOC=S△COF+S梯形ACFE-S△AOE,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| a |
| 1 |
| 2 |
=4+
| 16-a2 |
| a |
=
| 16-a2 |
| a |
∵△AOC的面积为6,
∴
| 16-a2 |
| a |
 整理得,a2+6a-16=0,
整理得,a2+6a-16=0,解得a1=2,a2=-8(舍去),
∴
| 8 |
| a |
| 8 |
| 2 |
∴点C的坐标为(2,4).
若S△AOC=S△AOE+S梯形ACFE-S△COF=
| a2-16 |
| a |
∴
| a2-16 |
| a |
解得:a=8或a=-2(舍去)
∴点C的坐标为(8,1).
故答案为:(2,4)或(8,1).
点评:本题考查了反比例函数与一次函数的交点问题,反比例函数系数的几何意义,作辅助线并表示出△ABC的面积是解题的关键.

练习册系列答案
相关题目
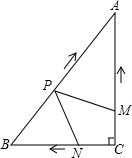 (2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(2013•遵义)如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).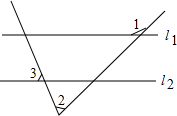 (2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )
(2013•遵义)如图,直线l1∥l2,若∠1=140°,∠2=70°,则∠3的度数是( )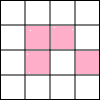 (2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )
(2013•遵义)如图,在4×4正方形网格中,任选取一个白色的小正方形并涂红,使图中红色部分的图形构成一个轴对称图形的概率是( )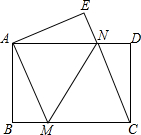 (2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(2013•遵义)如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N. (2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-
(2013•遵义)如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-