题目内容
【题目】如图,点A的坐标为(﹣1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 . 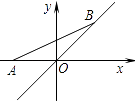
【答案】(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】解:先过点A作AB′⊥OB,垂足为点B′,
由垂线段最短可知,当B′与点B重合时AB最短,
∵点B在直线y=x上运动,
∴△AOB′是等腰直角三角形,
过B′作B′C⊥x轴,垂足为C,
∴△B′CO为等腰直角三角形,
∵点A的坐标为(﹣1,0),
∴OC=CB′= ![]() OA=
OA= ![]() ×1=
×1= ![]() ,
,
∴B′坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),
),
即当线段AB最短时,点B的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).
).
故答案为:(﹣ ![]() ,﹣
,﹣ ![]() ).
).
先过点A作AB′⊥OB,垂足为点B′,由于点B在直线y=x上运动,所以△AOB′是等腰直角三角形,由勾股定理求出OB′的长即可得出点B′的坐标.

练习册系列答案
相关题目