题目内容

（2013•梧州一模）如图，九年级数学兴趣小组测量升旗台上旗杆的高度，他们在观测点B处测得A点仰角∠DBA=30°，测得C点的仰角∠DBC=70°，AB=4米．求旗杆上AC的高（精确到0.1米）．（参考数据：sin70°=0.9397，cos70°=0.3420，tan70°=2.7475，
3
=1.732）
分析：在Rt△ABD中利用三角函数求得AD的长，则根据勾股定理即可求得BD的长，然后在直角△CBD中，利用三角函数求得CD的长，则AC即可求解．
解答：解：在Rt△ABD中，∠DBA=30°，AB=4
∴AD=
1
2
AB=2，
∴BD=
AB2-AD2
=2
3
．
在Rt△CBD中，∠DBC=70°
CD=BD•tan∠DBC=2
3
•tan70°=2×1.732×2.7475=9.5173，
AC=CD-AD=9.5173-2≈7.5（米）．
答：旗杆上AC的高约是7.5米．
点评：此题主要考查了仰角与俯角的问题，利用两个直角三角形拥有公共直角边，能够合理的运用这条公共边是解答此题的关键．
练习册系列答案
相关题目
（2013•梧州一模）用科学记数法表示2175000000为（　　）
（2013•梧州一模）一组数据2、0、3、2、3、1、x的众数是3，则这组数据从小到大排列的中位数是
2
2
．
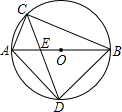（2013•梧州一模）已知在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，交AB于E，则CD的长是
7
2
7
2
．
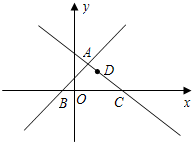（2013•梧州一模）如图，在平面直角坐标系xOy中，直线y=x+1与y=-
3
4
x+3交于点A，分别交x轴于点B和点C，点D是直线AC上且位于y轴右侧的一个动点．
（1）点A，B，C的坐标是A
（
8
7
，
15
7
）
（
8
7
，
15
7
）
，B
（-1，0）
（-1，0）
，C
（4，0）
（4，0）
．
（2）当△CBD为等腰三角形时，点D的坐标是
（
3
2
，
15
8
）或（8，-3）
（
3
2
，
15
8
）或（8，-3）
．
（3）在（2）中，当点D在第四象限时，过点D的反比例函数解析式是
y=-
24
x
y=-
24
x
．
（2013•梧州一模）如图，在3×3的正方形网格中，每个小正方形的边长为1，A、B两点在网格格点上，若C点也在网格格点上，以A、B、C三点为顶点的三角形的面积为1，则满足条件的点C的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网