题目内容
如图①在正方形网格中有四边形ABCD。
(1)利用网格作∠A、∠B的平分线;
(2)∠A、∠B的平分线交于点O,判断点O是否在其他两个角的平分线上;
(3)从图中得出的结论:①AD∥BC;②∠AOB=∠DOC=90°;③AD+BC=AB+CD;④S△AOB=S△COD;⑤∠AOD与∠BOC互补;其中正确的结论为_____________(写序号);
(4)如图②,在四边形ABCD中四个内角平分线仍相交于一点O,在(3)的正确结论中,哪些仍然成立?成立的请说明理由。

| 解:(1)如图; (2)在; (3)结论有 ①AD∥BC;②∠AOB=∠DOC=90°;③AD+BC=AB+CO;⑤∠ADD与∠BOC互补; (4) ③AD+BC=AB+CO依然成立; ③过点O向四边作垂线,垂足为E、F、G、H, 根据角平分线的性质,AE=AF,DE=DH,BF=BG,CG=CH, 所以,AD+BC=AE+DE+BG+GC=AF+DH+BF+CH=AB+CD。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
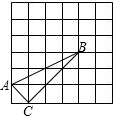 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
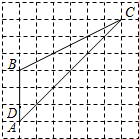 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
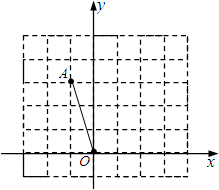 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).