题目内容
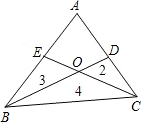如图，D、E分别是ABC的AC、AB边上的点，BD、CE相交于点O，若S△OCD=2，S△OBE=3，S△OBC=4，那么SADOE=分析：作BO的中点F，易知：S△BFC=S△OFC=S△ODC，可得出BF=OF=OD，即：S△BFE=S△EOF=S△OED=
S△OBE，根据三角形的面积公式将
△AED的面积S的代数式表示出来，列出式子求出S的值，S+S△OED即为SADOE的值．
| 1 |
| 2 |
| AD |
| DC |
解答：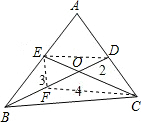
解：如图所示：作BO的中点F，连接CF、EF、ED．
易知：S△BFC=S△OFC=
S△OBC=2=S△ODC，
即：BF=OF=OD，
所以可得：S△BFE=S△EOF=S△OED=
S△OBE=
，
设△AED的面积为S，则
S△ABD=S△OBE+S△OED+S△AED=3+
+S=
+S，
S△BDC=S△OBC+S△ODC=6，
S△CED=S△OED+S△ODC=
+2=
，
由三角形的面积公式可得：
=
=
=
，
=
=
=
，
即：
=
，S=
=6.3，
SADOE=S+S△OED=6.3+
=7.8．
故答案为7.8．
解：如图所示：作BO的中点F，连接CF、EF、ED．易知：S△BFC=S△OFC=
| 1 |
| 2 |
即：BF=OF=OD，
所以可得：S△BFE=S△EOF=S△OED=
| 1 |
| 2 |
| 3 |
| 2 |
设△AED的面积为S，则
S△ABD=S△OBE+S△OED+S△AED=3+
| 3 |
| 2 |
| 9 |
| 2 |
S△BDC=S△OBC+S△ODC=6，
S△CED=S△OED+S△ODC=
| 3 |
| 2 |
| 7 |
| 2 |
由三角形的面积公式可得：
| SABD |
| SBDC |
| AD |
| DC |
| ||
| 6 |
| 9+2S |
| 12 |
| SAED |
| SEDC |
| AD |
| DC |
| S | ||
|
| 2S |
| 7 |
即：
| 2S |
| 7 |
| 9+2S |
| 12 |
| 63 |
| 10 |
SADOE=S+S△OED=6.3+
| 3 |
| 2 |
故答案为7.8．
点评：本题主要考查了三角形面积公式的灵活应用，巧妙点在于运用三等分点求出面积相等的部分，即求出未知面积的区域．
练习册系列答案
相关题目
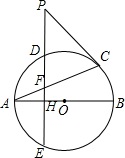如图：AB、AC分别是⊙O的直径和弦，D为弧AC上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F．P为ED延长线上一点，连PC．
如图，AB和AC分别是⊙O的直径和弦，OD⊥AC于D点，若OA=4，∠A=30°，则BD等于（ ）
已知：如图，E、F分别是正方形ABCD边BC、AD上的点，且BE=DF
桌上放着一个圆柱和一个长方体，如图（1），请说出下列三幅图（如图（2））分别是从哪个方向看到的．