题目内容
【题目】如图,在梯形ABCD中, ![]() 利用面积法证明勾股定理.
利用面积法证明勾股定理.

【答案】证明见解析.
【解析】试题分析:
用以下两种方法分别计算梯形ABCD的面积,再利用同一个几何图形的面积相等得到等式变形即可证明得到“勾股定理”;
方法(1):S梯形=![]() (上底+下底)
(上底+下底) ![]() 高;方法(2):S梯形=S△ABE+S△ADC+S△BCE;
高;方法(2):S梯形=S△ABE+S△ADC+S△BCE;
试题解析:
由题意可得:在△ADE和△ECB中, 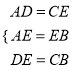 ,
,
∴△ADE≌△ECB,
∴∠AED=∠EBC,
∵EBC+∠BEC=90°,
∴∠AED+∠BEC=90°,
∴∠AEB=90°.
∴(1):S梯形=![]() (上底+下底)
(上底+下底) ![]() 高=
高=![]() ;
;
(2):S梯形=S△ABE+S△ADC+S△BCE=![]() ;
;
∴![]() 即:
即: ![]() ,
,
∴![]() .
.
即:在直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目



