题目内容
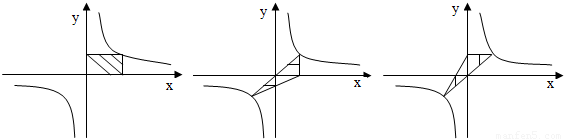
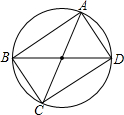
 如图,顺次连接任意四边形ABCD各边中点E、F、G、H得到的四边形是一个特殊四边形,它是________形.
如图,顺次连接任意四边形ABCD各边中点E、F、G、H得到的四边形是一个特殊四边形,它是________形.
平行四边
分析:连接AC,根据三角形的中位线得到HG∥AC,HG= AC,EF∥AC,EF=
AC,EF∥AC,EF= AC,推出EF=GH,EF∥GH,根据平行四边形的判定求出即可.
AC,推出EF=GH,EF∥GH,根据平行四边形的判定求出即可.
解答: 解:它是平行四边形,
解:它是平行四边形,
理由是:连接AC,
∵四边形ABCD各边中点是E、F、G、H,
∴HG∥AC,HG= AC,EF∥AC,EF=
AC,EF∥AC,EF= AC,
AC,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
故答案为:平行四边.
点评:本题主要考查对平行四边形的判定,三角形的中位线,平行公理及推论等知识点的理解和掌握,能推出EF=GH和EF∥GH是解此题的关键.
分析:连接AC,根据三角形的中位线得到HG∥AC,HG=
 AC,EF∥AC,EF=
AC,EF∥AC,EF= AC,推出EF=GH,EF∥GH,根据平行四边形的判定求出即可.
AC,推出EF=GH,EF∥GH,根据平行四边形的判定求出即可.解答:
 解:它是平行四边形,
解:它是平行四边形,理由是:连接AC,
∵四边形ABCD各边中点是E、F、G、H,
∴HG∥AC,HG=
 AC,EF∥AC,EF=
AC,EF∥AC,EF= AC,
AC,∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形.
故答案为:平行四边.
点评:本题主要考查对平行四边形的判定,三角形的中位线,平行公理及推论等知识点的理解和掌握,能推出EF=GH和EF∥GH是解此题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
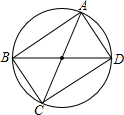
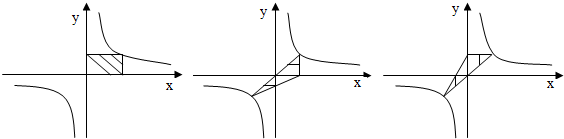

 的图象中,下列阴影部分的面积均为1;(见下图)
的图象中,下列阴影部分的面积均为1;(见下图)
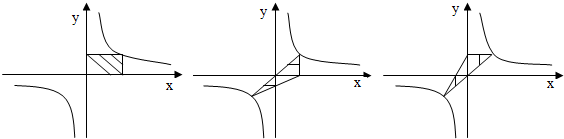
 的图象中,下列阴影部分的面积均为1;(见下图)
的图象中,下列阴影部分的面积均为1;(见下图)