题目内容
深化理解(本小题满分9分)
如图,在平面直角坐标系中,点C的坐标为(0,4),A是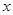 轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作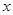 轴的垂线、过点C作
轴的垂线、过点C作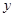 轴的垂线,两直线交于点D,直线DB交
轴的垂线,两直线交于点D,直线DB交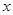 轴于一点E.
轴于一点E.
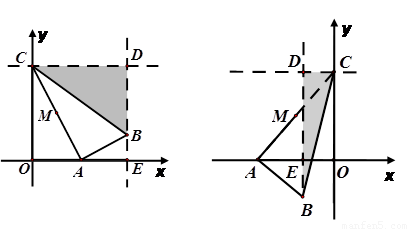
设A点的横坐标为 ,
,
(1)若 =3,则点B的坐标为
▲ ,若
=3,则点B的坐标为
▲ ,若 =-3,,则点B的坐标为 ▲ ;
=-3,,则点B的坐标为 ▲ ;
(2)若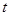 >0,△BCD的面积为
>0,△BCD的面积为 ,则
,则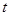 为何值时,
为何值时,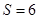 ?
?
(3)是否存在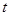 ,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时
,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时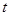 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)(5, 1.5 ) , (-1, -1.5 );(2)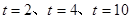 (3)
(3)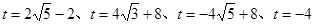 ,理由见解析
,理由见解析
【解析】(1)(5, 1.5 ) , (-1, -1.5 );
(2)①当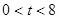 时,如图(1)
时,如图(1)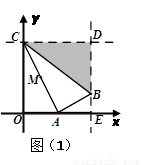
△AOC∽△BEA且相识比为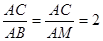
求得点B的坐标为(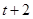 ,
,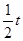 )
) 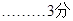
∴
解得 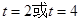
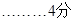
②当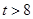 时,如图(2)
时,如图(2)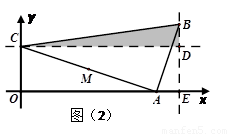
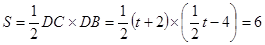
解得 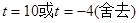
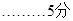
∴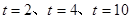
(3)①当 时,如图(1)
时,如图(1)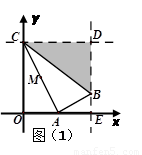
若△AOC∽△CDB
∴ 即:
即:
∴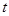 无解
无解
若△AOC∽△BDC,同理,解得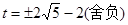
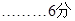
②当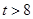 时,如图(2)
时,如图(2)
若△AOC∽△CDB,
∴ 即:
即: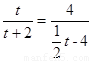
解得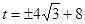 ,取
,取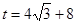
若△AOC∽△BDC,同理,解得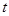 无解
无解
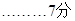
③当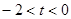 时,如图(3)
时,如图(3)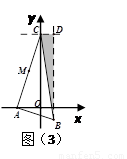
若△AOC∽△CDB
∴ 即:
即: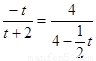
解得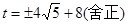
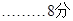
若△AOC∽△BDC,同理,解得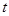 无解
无解
④当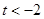 时,如图(4)
时,如图(4)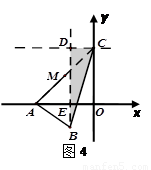
若△AOC∽△CDB
∴ 即:
即: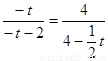
∴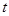 无解
无解
若△AOC∽△BDC,同理,解得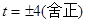
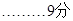
∴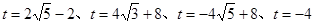
(1)根据勾股定理和对称性求解
(2)求△BCD的面积时,可以CD为底、BD为高来解,那么表示出BD的长是关键;
Rt△CAO∽Rt△ABE,且知道AC、AB的比例关系,即可通过相似三角形的对应边成比例求出BE的长,进一步得到BD的长,在表达BD长时,应分两种情况考虑:①B在线段DE上,②B在ED的延长线上.
(3)通过B点所在的不同位置,分四种情况解答

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作
轴上的一个动点,M是线段AC的中点.把线段AM进行以A为旋转中心、向顺时针方向旋转90°的旋转变换得到AB.过B作 轴的垂线,两直线交于点D,直线DB交
轴的垂线,两直线交于点D,直线DB交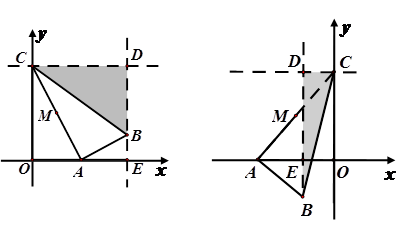
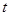 ,
,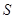 ,则
,则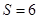 ?
?