题目内容
阅读材料:善于思考的小军在解方程组 时,采用了一种“整体代换”的解法:
解:将方程②变形:4x+10y+y=5 即 2+y=5③
把方程①带入③得:2×3+y=5,∴y=﹣1
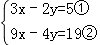 把 y=﹣1 代入①得 x=4,∴方程组的解为
把 y=﹣1 代入①得 x=4,∴方程组的解为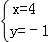 . 请你解决以下问题:
. 请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组
 已知 x,y 满足方程组 .
已知 x,y 满足方程组 .
(i)求 x2+4y2 的值;
(ii)求 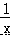 +
+ 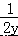 的值.
的值.
【考点】解二元一次方程组.
【专题】阅读型;新定义;整体思想.
【分析】(1)模仿小军的“整体代换”法,求出方程组的解即可; 方程组整理后,模仿小军的“整体代换”法,求出所求式子的值即可.
【解答】解:(1)把方程②变形:3(3x﹣2y)+2y=19③, 把①代入③得:15+2y=19,即 y=2,
 把 y=2 代入①得:x=3, 则方程组的解为 ;
把 y=2 代入①得:x=3, 则方程组的解为 ;
(i)由①得:3(x2+4y2)=47+2xy,即 x2+4y2=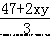 ③, 把③代入②得:2×
③, 把③代入②得:2× 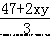 =36﹣xy,
=36﹣xy,
解得:xy=2,
则 x2+4y2=17;
(ii)∵x2+4y2=17,
∴(x+2y)2=x2+4y2+4xy=17+8=25,
∴x+2y=5 或 x+2y=﹣5,
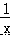
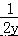
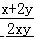
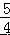 则 + = =± .
则 + = =± .
【点评】此题考查了解二元一次方程组,弄清阅读材料中的“整体代入”方法是解本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
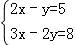 解方程组 .
解方程组 .